题目内容
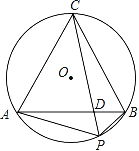
【题目】如图,在平行四边形ABCD中,![]() ,垂足为点E,以AE为直径的
,垂足为点E,以AE为直径的![]() 与边CD相切于点F,连接BF交
与边CD相切于点F,连接BF交![]() 于点G,连接EG.
于点G,连接EG.
(1)求证:![]() .
.
(2)若![]() ,求
,求![]() 的值.
的值.

【答案】(1)见解析;(2)![]() .
.
【解析】
(1)证明![]() ,可得AD是
,可得AD是![]() 的切线,由切线长定理得
的切线,由切线长定理得![]() ,同理
,同理![]() ,则
,则![]() ;
;
(2)连接OD,AF相交于点M,设![]() ,则
,则![]() ,求得
,求得![]() ,
,![]() ,可求出
,可求出![]() ,证得
,证得![]() ,求出
,求出![]() ,可证明
,可证明![]() ,则
,则![]() 可求出.
可求出.
(1)证明:∵四边形ABCD是平行四边形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵AO是![]() 的半径,
的半径,
∴AD是![]() 的切线,
的切线,
又∵DF是![]() 的切线,
的切线,
∴![]() ,
,
同理可得![]() ,
,
∵![]() ,
,
∴![]() .
.
(2)解:连接OD,AF相交于点M,

∵四边形ABCD是平行四边形,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴设![]() ,则
,则![]() ,
,
∴![]() ,
,![]() ,
,
∴在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵DA,DF是![]() 的两条切线,
的两条切线,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴在![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?