题目内容
【题目】如图1,一扇窗户打开一定角度,其中一端固定在窗户边OM上的点A处,另一端B在边ON上滑动,图2为某一位置从上往下看的平面图,测得∠ABO为37°,∠AOB为45°,OB长为35厘米,求AB的长(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
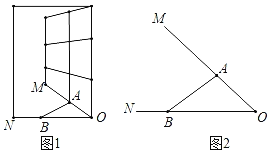
【答案】AB的长为25厘米
【解析】
作AC⊥OB于点C,然后根据题意和锐角三角函数可以求得AC和BC的长,再根据勾股定理即可得到AB的长,本题得以解决.
作AC⊥OB于点C,如图2所示,
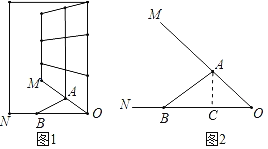
则∠ACO=∠ACB=90°,
∵∠AOC=45°,
∴∠AOC=∠COA=45°,
∴AC=OC,
设AC=x,则OC=x,BC=35﹣x,
∵∠ABC=37°,tan37°≈0.75,
∴![]() =0.75,
=0.75,
解得,x=15,
∴35﹣x=20,
∴AB=![]() =25(厘米),
=25(厘米),
即AB的长为25厘米.

练习册系列答案
相关题目
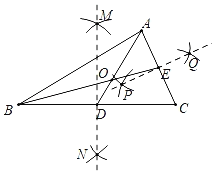
【题目】已知在ABC中,小明按照下列作图步骤进行尺规作图(示意图与作图步骤如表),那么交点O是△ABC的( )
示意图 | 作图步骤 |
| (1)分别以点B、C为圆心,大于 (2)分别以点A、C为圆心,大于 (3)联结AD、BE,相交于点O |
A.外心B.内切圆的圆心C.重心D.中心