��Ŀ����
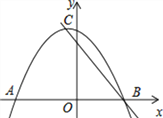
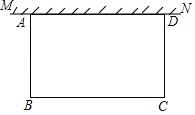
����Ŀ����ͼ1�����߳�Ϊ1��������ABCDѹ��Ϊ�߳�Ϊ1������ABCD��������ABCD�У���A�Ĵ�СΪ���������ΪS��
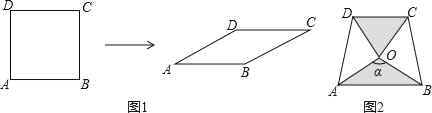
��1���벹ȫ����
�� | 30�� | 45�� | 60�� | 90�� | 120�� | 135�� | 150�� |
S |
| 1 |
|
��2����գ�
�ɣ�1�����Է��ֵ�λ��������ѹ��Ĺ����У����ε�������š�A��С�ı仯���仯�������ѵ�λ���ε����S��ΪS�����������磺������30��ʱ��S��S��30�㣩��![]() ��������135��ʱ��S��S��135�㣩��
��������135��ʱ��S��S��135�㣩��![]() �����ϱ����Եõ�S��60�㣩��S���� ���㣩��S��150�㣩��S���� ���㣩�������ɴ˿��Թ��ɳ�S��180�㩁���������� ���㣩��
�����ϱ����Եõ�S��60�㣩��S���� ���㣩��S��150�㣩��S���� ���㣩�������ɴ˿��Թ��ɳ�S��180�㩁���������� ���㣩��
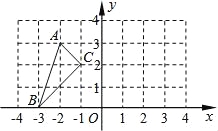
��3��������ͬ�ĵ���ֱ�����ǰ尴ͼ2�ķ�ʽ���ã�AD��![]() ����AOB��������̽��ͼ����������Ӱ������������Ƿ���ȣ���˵�����ɣ�ע���������ã�2���еĽ��ۣ���
����AOB��������̽��ͼ����������Ӱ������������Ƿ���ȣ���˵�����ɣ�ע���������ã�2���еĽ��ۣ���
���𰸡���1��![]() ��2��120��30������3����������Ӱ��������������
��2��120��30������3����������Ӱ��������������
��������
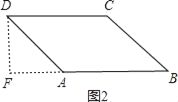
��1����D��DE��AB�ڵ�E��������45��ʱ�������DE���Ӷ���������ε����S��ͬ����������60��ʱS��ֵ��������120��ʱ����D��DF��AB��BA���ӳ����ڵ�F��������DF�������S��ֵ��ͬ��������135��ʱS��ֵ��
��2�����ݱ������������S��ֵ���ɵó��𰸣�
��3������ABO��AB���۵õ�����AEBO������CDO��CD���۵õ�����OCFD�����ã�2���еĽ��ۣ�����á�AOB�͡�COD��������Ӷ�����ý��ۣ�
�⣺��1��������45��ʱ����ͼ1����D��DE��AB�ڵ�E��

��DE��![]() AD��
AD��![]() ��
��
��S��ABDE��![]() ��
��
ͬ��������60��ʱS��![]() ��
��
������120��ʱ����ͼ2����D��DF��AB����BA���ӳ����ڵ�F��
���DAE��60�㣬
��DF��![]() AD��
AD��![]() ��
��
��S��ABDF��![]() ��
��
ͬ��������150��ʱ�������S��![]() ��
��
�ʱ���������д��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��2���ɣ�1����֪S��60�㣩��S��120�㣩��
S��150�㣩��S��30�㣩��
��S��180�㩁������S������
�ʴ�Ϊ��120��30������
��3����������Ӱ�������������ȣ�
֤������ͼ3����ABO��AB���۵õ�����AMBO������CDO��CD���۵õ�����OCND��
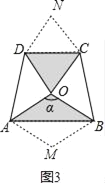
�ߡ�AOD����COB��90�㣬
���COD+��AOB��180�㣬
��S��AOB��![]() S����AMBO��
S����AMBO��![]() S������
S������
S��CDO��![]() S����OCND��
S����OCND��![]() S��180�㩁����
S��180�㩁����
�ɣ�2���н���S��������S��180�㩁����
��S��AOB��S��CDO��

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ��ijУ���꼶��֯��ѧ���껪�����������������꼶��������һЩ��Ʒ���б��ã����ͳ�ƽ�����±�������������ʾ��
һ�Ƚ� | ���Ƚ� | ���Ƚ� | �ϼ� | |
������(�����) | 40 | |||
��Ʒ����(��λ��Ԫ) | 12 | 9 | 6 | |
��Ʒ���(��λ��Ԫ) | 300 |
��֪���Ƚ��Ļ�������һ�Ƚ��Ļ�������5�ˣ����ܸ��������������ֱ�������ֽ���Ļ�������������������δ֪���������(����ʽ���ػ���)�����з��̽��