ΧβΡΩΡΎ»ί
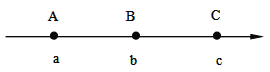
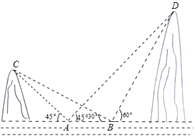
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ ΐ÷α…œΒψA±μ Ψ ΐaΘ§ΒψC±μ Ψ ΐcΘ§«“Εύœν Ϋx3+15x2y2©¹20ΒΡ≥Θ ΐœν «aΘ§ΉνΗΏ¥ΈœνΒΡœΒ ΐ «cΘ°Έ“Ο«Α― ΐ÷α…œΝΫΒψ÷°ΦδΒΡΨύάκ”Ο±μ ΨΝΫΒψΒΡ¥σ–¥Ή÷ΡΗ“ΜΤπ±ξΦ«Θ°±»»γΘ§ΒψA”κΒψB÷°ΦδΒΡΨύάκΦ«ΉςABΘ°
Θ®1Θ©«σaΘ§cΒΡ÷ΒΘΜ
Θ®2Θ©Ε·ΒψB¥” ΐ©¹6Ε‘”ΠΒΡΒψΩΣ Φœρ”“‘ΥΕ·Θ§ΥΌΕ»ΈΣΟΩΟκ2ΗωΒΞΈΜ≥ΛΕ»Θ°Ά§ ±ΒψAΘ§C‘Ύ ΐ÷α…œ‘ΥΕ·Θ§ΒψAΘ§CΒΡΥΌΕ»Ζ÷±πΈΣΟΩΟκ3ΗωΒΞΈΜ≥ΛΕ»Θ§ΟΩΟκ4ΗωΒΞΈΜ≥ΛΕ»Θ§…η‘ΥΕ· ±ΦδΈΣtΟκΘ°
ΔΌ»τΒψAœρ”“‘ΥΕ·Θ§ΒψCœρΉσ‘ΥΕ·Θ§ABΘΫBCΘ°«σtΒΡ÷ΒΘΜ
ΔΎ»τΒψAœρΉσ‘ΥΕ·Θ§ΒψCœρ ·‘ΥΕ·Θ§2AB©¹mBCΒΡ÷Β≤ΜΥφ ±ΦδtΒΡ±δΜ·ΕχΗΡ±δΘ§«σ≥ωmΒΡ÷ΒΘ°
![]()
ΓΨ¥πΑΗΓΩΘ®1Θ©aΘΫ©¹20Θ§cΘΫ15ΘΜΘ®2Θ©ΔΌtΒΡ÷ΒΈΣ![]() Μρ5ΘΜΔΎmΒΡ÷ΒΈΣ5Θ°
Μρ5ΘΜΔΎmΒΡ÷ΒΈΣ5Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΕύœν ΫΒΡΕ®“εΘ§Ω…«σ≥ωaΘ§cΒΡ÷ΒΘΜ
Θ®2Θ©ΔΌΒ±‘ΥΕ· ±ΦδΈΣtΟκ ±Θ§ΒψA±μ ΨΒΡ ΐΈΣ3t©¹20Θ§ΒψB±μ ΨΒΡ ΐΈΣ2t©¹6Θ§ΒψC±μ ΨΒΡ ΐΈΣ©¹4t+15Θ§ΗυΨίABΘΫBCΘ§Φ¥Ω…ΒΟ≥ωΙΊ”ΎtΒΡΚ§ΨχΕ‘÷ΒΖϊΚ≈ΒΡ“Μ‘Σ“Μ¥ΈΖΫ≥ΧΘ§Ϋβ÷°Φ¥Ω…ΒΟ≥ωΫα¬έΘΜ
ΔΎΒ±‘ΥΕ· ±ΦδΈΣtΟκ ±Θ§ΒψA±μ ΨΒΡ ΐΈΣ©¹3t©¹20Θ§ΒψB±μ ΨΒΡ ΐΈΣ2t©¹6Θ§ΒψC±μ ΨΒΡ ΐΈΣ4t+15Θ§ΫχΕχΩ…ΒΟ≥ωABΘΫ5t+14Θ§BCΘΫ2t+21Θ§ΫαΚœ2AB©¹mBCΒΡ÷Β≤ΜΥφ ±ΦδtΒΡ±δΜ·ΕχΗΡ±δΘ§Ω…ΒΟ≥ωΙΊ”ΎmΒΡ“Μ‘Σ“Μ¥ΈΖΫ≥ΧΘ§Ϋβ÷°Φ¥Ω…ΒΟ≥ωΫα¬έΘ°
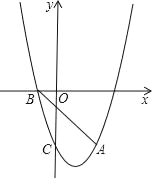
Θ®1Θ©ΓΏΕύœν Ϋx3+15x2y2©¹20ΒΡ≥Θ ΐœν «aΘ§ΉνΗΏ¥ΈœνΒΡœΒ ΐ «cΘ§
ΓύaΘΫ©¹20Θ§cΘΫ15Θ°
Θ®2Θ©ΔΌΒ±‘ΥΕ· ±ΦδΈΣtΟκ ±Θ§ΒψA±μ ΨΒΡ ΐΈΣ3t©¹20Θ§ΒψB±μ ΨΒΡ ΐΈΣ2t©¹6Θ§ΒψC±μ ΨΒΡ ΐΈΣ©¹4t+15Θ§
ΓΏABΘΫBCΘ§
Γύ|3t©¹20©¹Θ®2t©¹6Θ©|ΘΫ|2t©¹6©¹Θ®©¹4t+15Θ©|Θ§Φ¥t©¹14ΘΫ6t©¹21Μρt©¹14ΘΫ21©¹6tΘ§
ΫβΒΟΘΚtΘΫ![]() ΜρtΘΫ5Θ°
ΜρtΘΫ5Θ°
¥πΘΚtΒΡ÷ΒΈΣ![]() Μρ5Θ°
Μρ5Θ°
ΔΎΒ±‘ΥΕ· ±ΦδΈΣtΟκ ±Θ§ΒψA±μ ΨΒΡ ΐΈΣ©¹3t©¹20Θ§ΒψB±μ ΨΒΡ ΐΈΣ2t©¹6Θ§ΒψC±μ ΨΒΡ ΐΈΣ4t+15Θ§
ΓύABΘΫ|©¹3t©¹20©¹Θ®2t©¹6Θ©|ΘΫ5t+14Θ§BCΘΫ|2t©¹6©¹Θ®4t+15Θ©|ΘΫ2t+21Θ§
Γύ2AB©¹mBCΘΫ10t+14©¹2mt©¹21mΘΫΘ®10©¹2mΘ©t+14©¹21mΘ°
ΓΏ2AB©¹mBCΒΡ÷Β≤ΜΥφ ±ΦδtΒΡ±δΜ·ΕχΗΡ±δΘ§
Γύ10©¹2mΘΫ0Θ§
ΓύmΘΫ5Θ°
¥πΘΚmΒΡ÷ΒΈΣ5Θ°

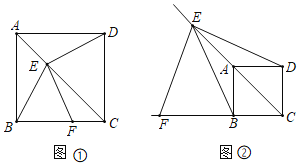
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§ΫΪ±Ώ≥ΛΈΣ1ΒΡ’ΐΖΫ–ΈABCD―Ι±βΈΣ±Ώ≥ΛΈΣ1ΒΡΝβ–ΈABCDΘ°‘ΎΝβ–ΈABCD÷–Θ§ΓœAΒΡ¥σ–ΓΈΣΠΝΘ§ΟφΜΐΦ«ΈΣSΘ°
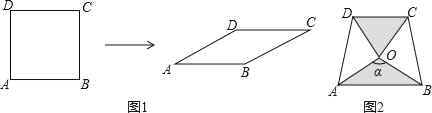
Θ®1Θ©«κ≤Ι»Ϊ±μΘΚ
ΠΝ | 30Γψ | 45Γψ | 60Γψ | 90Γψ | 120Γψ | 135Γψ | 150Γψ |
S |
| 1 |
|
Θ®2Θ©ΧνΩ’ΘΚ
”…Θ®1Θ©Ω…“‘ΖΔœ÷ΒΞΈΜ’ΐΖΫ–Έ‘Ύ―Ι±βΒΡΙΐ≥Χ÷–Θ§Νβ–ΈΒΡΟφΜΐΥφΉ≈ΓœA¥σ–ΓΒΡ±δΜ·Εχ±δΜ·Θ§≤ΜΖΝΑ―ΒΞΈΜΝβ–ΈΒΡΟφΜΐSΦ«ΈΣSΘ®ΠΝΘ©Θ°άΐ»γΘΚΒ±ΠΝΘΫ30Γψ ±Θ§SΘΫSΘ®30ΓψΘ©ΘΫ![]() ΘΜΒ±ΠΝΘΫ135Γψ ±Θ§SΘΫSΘ®135ΓψΘ©ΘΫ
ΘΜΒ±ΠΝΘΫ135Γψ ±Θ§SΘΫSΘ®135ΓψΘ©ΘΫ![]() Θ°”……œ±μΩ…“‘ΒΟΒΫSΘ®60ΓψΘ©ΘΫSΘ®ΓΓ ΓΓΓψΘ©ΘΜSΘ®150ΓψΘ©ΘΫSΘ®ΓΓ ΓΓΓψΘ©Θ§Γ≠Θ§”…¥ΥΩ…“‘ΙιΡ…≥ωSΘ®180Γψ©¹ΠΝΘ©ΘΫΘ®ΓΓ ΓΓΓψΘ©Θ°
Θ°”……œ±μΩ…“‘ΒΟΒΫSΘ®60ΓψΘ©ΘΫSΘ®ΓΓ ΓΓΓψΘ©ΘΜSΘ®150ΓψΘ©ΘΫSΘ®ΓΓ ΓΓΓψΘ©Θ§Γ≠Θ§”…¥ΥΩ…“‘ΙιΡ…≥ωSΘ®180Γψ©¹ΠΝΘ©ΘΫΘ®ΓΓ ΓΓΓψΘ©Θ°
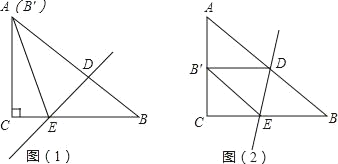
Θ®3Θ©ΝΫΩιœύΆ§ΒΡΒ»―ϋ÷±Ϋ«»ΐΫ«ΑεΑ¥ΆΦ2ΒΡΖΫ ΫΖ≈÷ΟΘ§ADΘΫ![]() Θ§ΓœAOBΘΫΠΝΘ§ ‘ΧΫΨΩΆΦ÷–ΝΫΗω¥χ“θ”ΑΒΡ»ΐΫ«–ΈΟφΜΐ «ΖώœύΒ»Θ§≤ΔΥΒΟςάμ”…Θ®ΉΔΘΚΩ…“‘άϊ”ΟΘ®2Θ©÷–ΒΡΫα¬έΘ©Θ°
Θ§ΓœAOBΘΫΠΝΘ§ ‘ΧΫΨΩΆΦ÷–ΝΫΗω¥χ“θ”ΑΒΡ»ΐΫ«–ΈΟφΜΐ «ΖώœύΒ»Θ§≤ΔΥΒΟςάμ”…Θ®ΉΔΘΚΩ…“‘άϊ”ΟΘ®2Θ©÷–ΒΡΫα¬έΘ©Θ°