题目内容
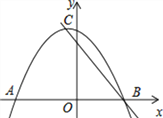
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣2,0)、B(x1,0),且1<x1<2,与y轴正半轴的交点在(0,2)的上方,顶点为C.直线y=kx+m(k≠0)经过点C、B.则下列结论:①b>a;②2a﹣b>﹣1;③2a+c<0;④k>a+b;⑤k<﹣1. 其中正确的结论有_________.(填序号)
【答案】①⑤
【解析】①、因为图象与x轴两交点为(-2,0),(x1,0),且1<x1<2,
对称轴x= ![]() ,
,
则对称轴![]() ,且a<0,∴b>a,①正确;
,且a<0,∴b>a,①正确;
②、由抛物线过(-2,0),则4a-2b+c=0,而c>2,则4a-2b+2<0,即2a-b+1<0,2a-b<-1,②错误;
③、设x2=-2,则x1x2=![]() ,而1<x1<2,
,而1<x1<2,
∴-4<x1x2<-2,∴-4<![]() <-2,
<-2,
∴2a+c>0,4a+c<0,∴③错误;
④、由题意可知:当x=1时,a+b+c>k+m,
直线y=kx+m(k≠0)经过点C(0,2),所以m=2,
又c>2,
所以a+b>k,故④错误;
⑤、由题意:kx1+m=0,m=2,1<x1<2,
所以k=-![]() =
=![]() <-1,⑤正确,
<-1,⑤正确,
故答案为:①⑤.

 阅读快车系列答案
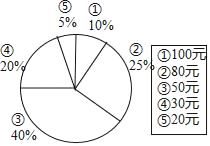
阅读快车系列答案【题目】某果品超市经销一种水果,已知该水果的进价为每千克15元,通过一段时间的销售情况发现,该种水果每周的销售总额相同,且每周的销售量y(千克)与每千克售价x(元)的关系如表所示
每千克售价x(元) | 25 | 30 | 40 |
每周销售量y(千克) | 240 | 200 | 150 |
(1)写出每周销售量y(千克)与每千克售价x(元)的函数关系式;
(2)由于销售淡季即将来临,超市要完成每周销售量不低于300千克的任务,则该种水果每千克售价最多定为多少元?
(3)在(2)的基础上,超市销售该种水果能否到达每周获利1200元?说明理由.
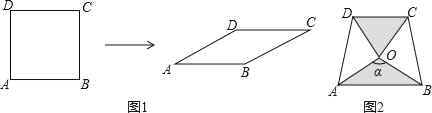
【题目】如图1,将边长为1的正方形ABCD压扁为边长为1的菱形ABCD.在菱形ABCD中,∠A的大小为α,面积记为S.
(1)请补全表:
α | 30° | 45° | 60° | 90° | 120° | 135° | 150° |
S |
| 1 |
|
(2)填空:
由(1)可以发现单位正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把单位菱形的面积S记为S(α).例如:当α=30°时,S=S(30°)=![]() ;当α=135°时,S=S(135°)=
;当α=135°时,S=S(135°)=![]() .由上表可以得到S(60°)=S( °);S(150°)=S( °),…,由此可以归纳出S(180°﹣α)=( °).
.由上表可以得到S(60°)=S( °);S(150°)=S( °),…,由此可以归纳出S(180°﹣α)=( °).
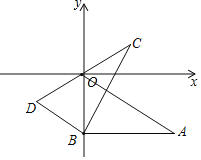
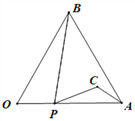
(3)两块相同的等腰直角三角板按图2的方式放置,AD=![]() ,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).