题目内容
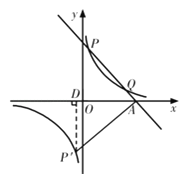
【题目】已知一次函数y=k1x+b与反比例函数y=![]() 的图象交于第一象限内的P(
的图象交于第一象限内的P(![]() ,8),Q(4,m)两点,与x轴交于A点.
,8),Q(4,m)两点,与x轴交于A点.
(1)分别求出这两个函数的表达式;
(2)写出点P关于原点的对称点P'的坐标;
(3)求∠P'AO的正弦值.
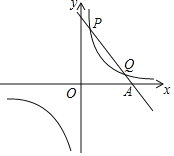
【答案】(1) 反比例函数的表达式为y=![]() ,一次函数的表达式为y=﹣2x+9;(2) (-
,一次函数的表达式为y=﹣2x+9;(2) (-![]() ,﹣8);(3)
,﹣8);(3) ![]() .
.
【解析】
试题分析:(1)根据P(![]() ,8),可得反比例函数解析式,根据P(
,8),可得反比例函数解析式,根据P(![]() ,8),Q(4,1)两点可得一次函数解析式;
,8),Q(4,1)两点可得一次函数解析式;
(2)根据中心对称的性质,可得点P关于原点的对称点P'的坐标;
(3)过点P′作P′D⊥x轴,垂足为D,构造直角三角形,依据P'D以及AP'的长,即可得到∠P'AO的正弦值.
试题解析:(1)∵点P在反比例函数的图象上,
∴把点P(![]() ,8)代入y=
,8)代入y=![]() 可得:k2=4,
可得:k2=4,
∴反比例函数的表达式为y=![]() ,
,
∴Q (4,1).
把P(![]() ,8),Q (4,1)分别代入y=k1x+b中,
,8),Q (4,1)分别代入y=k1x+b中,
得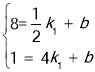 ,
,
解得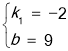 ,
,
∴一次函数的表达式为y=﹣2x+9;
(2)点P关于原点的对称点P'的坐标为(-![]() ,﹣8);
,﹣8);
(3)过点P′作P′D⊥x轴,垂足为D.
∵P′(-![]() ,﹣8),
,﹣8),
∴OD=![]() ,P′D=8,
,P′D=8,
∵点A在y=﹣2x+9的图象上,
∴点A(![]() ,0),即OA=
,0),即OA=![]() ,
,
∴DA=5,
∴P′A=![]() ,
,
∴sin∠P′AD=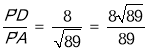 ,
,
∴sin∠P′AO= ![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】中国经济的快速发展让众多国家感受到了威胁,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示: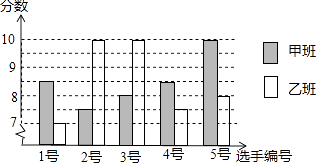
(1)根据上图填写下表:
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | ||
乙班 | 8.5 | 10 | 1.6 |
(2)根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.