题目内容
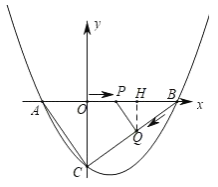
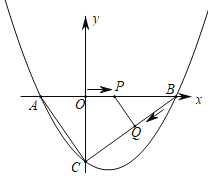
【题目】如图,抛物线与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当x=﹣1和x=3时,y值相等.直线y=![]() 与抛物线有两个交点,其中一个交点的横坐标是6,另一个交点是这条抛物线的顶点M.
与抛物线有两个交点,其中一个交点的横坐标是6,另一个交点是这条抛物线的顶点M.
(1)求这条抛物线的表达式.
(2)动点P从原点O出发,在线段OB上以每秒1个单位长度的速度向点B运动,同时点Q从点B出发,在线段BC上以每秒2个单位长度的速度向点C运动,当一个点到达终点时,另一个点立即停止运动,设运动时间为t秒.
①求t的取值范围.
②若使△BPQ为直角三角形,请求出符合条件的t值;
③t为何值时,四边形ACQP的面积有最小值,最小值是多少?直接写出答案.
【答案】(1)![]() ;(2)①
;(2)①![]() ,②t的值为
,②t的值为![]() 或
或![]() ,③当t=2时,四边形ACQP的面积有最小值,最小值是
,③当t=2时,四边形ACQP的面积有最小值,最小值是![]() .
.
【解析】
(1)求出对称轴,再求出y=![]() 与抛物线的两个交点坐标,将其代入抛物线的顶点式即可;
与抛物线的两个交点坐标,将其代入抛物线的顶点式即可;
(2)①先求出A、B、C的坐标,写出OB、OC的长度,再求出BC的长度,由运动速度即可求出t的取值范围;
②当△BPQ为直角三角形时,只存在∠BPQ=90°或∠PQB=90°两种情况,分别证△BPQ∽△BOC和△BPQ∽△BCO,即可求出t的值;
③如图,过点Q作QH⊥x轴于点H,证△BHQ∽△BOC,求出HQ的长,由公式S四边形ACQP=S△ABC-S△BPQ可求出含t的四边形ACQP的面积,通过二次函数的图象及性质可写出结论.
解:(1)∵在抛物线中,当x=﹣1和x=3时,y值相等,
∴对称轴为x=1,
∵y=![]() 与抛物线有两个交点,其中一个交点的横坐标是6,另一个交点是这条抛物线的顶点M,
与抛物线有两个交点,其中一个交点的横坐标是6,另一个交点是这条抛物线的顶点M,
∴顶点M(1,![]() ),另一交点为(6,6),
),另一交点为(6,6),
∴可设抛物线的解析式为y=a(x﹣1)2![]() ,
,
将点(6,6)代入y=a(x﹣1)2![]() ,
,
得6=a(6﹣1)2![]() ,
,
∴a=![]() ,
,
∴抛物线的解析式为![]()
(2)①在![]() 中,当y=0时,x1=﹣2,x2=4;当x=0时,y=﹣3,
中,当y=0时,x1=﹣2,x2=4;当x=0时,y=﹣3,
∴A(﹣2,0),B(4,0),C(0,﹣3),
∴在Rt△OCB中,OB=4,OC=3,
∴BC=![]() =5,
=5,
∴![]() ,
,
∵![]() <4,
<4,
∴![]()
②当△BPQ为直角三角形时,只存在∠BPQ=90°或∠PQB=90°两种情况,
当∠BPQ=90°时,∠BPQ=∠BOC=90°,
∴PQ∥OC,
∴△BPQ∽△BOC,
∴![]() ,即
,即![]() ,
,
∴t=![]() ;
;
当∠PQB=90°时,∠PQB=∠BOC=90°,∠PBQ=∠CBO,
∴△BPQ∽△BCO,
∴![]() ,即
,即![]() ,
,
∴t=![]() ,
,
综上所述,t的值为![]() 或
或![]() ;
;
③如右图,过点Q作QH⊥x轴于点H,
则∠BHQ=∠BOC=90°,
∴HQ∥OC,
∴△BHQ∽△BOC,
∴![]() ,即
,即![]() ,
,
∴HQ=![]() ,
,
∴S四边形ACQP=S△ABC﹣S△BPQ
=![]() ×6×3﹣
×6×3﹣![]() (4﹣t)×
(4﹣t)×![]() t
t
=![]() (t﹣2)2+
(t﹣2)2+![]() ,
,
∵![]() >0,
>0,
∴当t=2时,四边形ACQP的面积有最小值,最小值是![]() .
.