��Ŀ����
����Ŀ����ͼ�������������У�ÿ��С�����εı߳�����һ����λ���ȣ���ƽ��ֱ������ϵ�У���֪��ABC��������������ֱ���A����4��1����B����1��1����C����2��3����

��1������ABC����ƽ��1����λ���ȣ�������ƽ��3����λ���Ⱥ�õ���A1B1C1���뻭����A1B1C1��
��2������ABC��ԭ��O˳ʱ����ת90����õ���A2B2C2���뻭����A2B2C2��
��3��ֱ��д����C1��B1��B2Ϊ����������ε���״���� ����
���𰸡���1�������������A1��B1��C1������ֱ�Ϊ����3����2������0����2��������1��0������2�������������3������ֱ�������Σ�
��������
��1�����õ�ƽ�Ƶ���������д����A1��B1��C1�����꣬Ȼ����㼴�ɣ�
��2�����������ص����ת�����ʻ�����A��B��C�Ķ�Ӧ��A2��B2��C2�õ���A2B2C2��
��3�����ù��ɶ������涨�������жϣ�
�⣺��1����ͼ������ABC����ƽ��1����λ���ȣ�������ƽ��3����λ���ȣ����A1B1C1��Ϊ��������A1��B1��C1������ֱ�Ϊ����3����2������0����2��������1��0��
��2����ͼ��ÿ���㶼��ԭ��˳ʱ����ת90�㣬���A2B2C2��Ϊ������
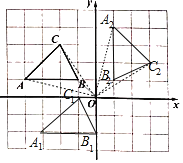
��3����C1B12��5��C1B22��5��B1B22��10��
��C1B12+C1B22��B1B22��C1B1��C1B2��
����C1��B1��B2Ϊ����������ε���״�ǵ���ֱ�������Σ�
�ʴ�Ϊ����ֱ�������Σ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�