Question

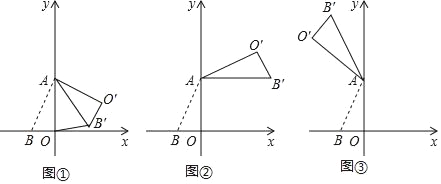
【题目】在平面直角坐标系中，O为原点，点A（0，4），点B（﹣2，0），把△ABO绕点A逆时针旋转，得△AB′O′，点B、O旋转后的对应点为B′、O′．

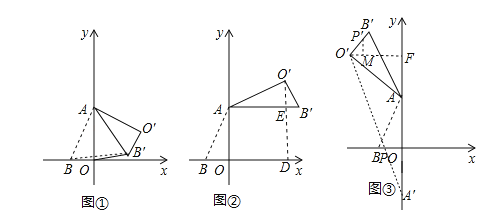
（1）如图①，若旋转角为60°时，求BB′的长；

（2）如图②，若AB′∥x轴，求点O′的坐标；

（3）如图③，若旋转角为240°时，边OB上的一点P旋转后的对应点为P′，当O′P+AP′取得最小值时，求点P′的坐标（直接写出结果即可）

Answer 1

【答案】（1）；（2）点O′的坐标为（，+4）；（3）点P′的坐标为（﹣，．

【解析】分析：（1）由点A、B的坐标可得出AB的长度，连接BB′，由旋转可知：AB=AB′，∠BAB′=60°，进而可得出△ABB′为等边三角形，根据等边三角形的性质可求出BB′的长；

（2）过点O′作O′D⊥x轴，垂足为D，交AB′于点E，则△AO′E∽△ABO，根据旋转的性质结合相似三角形的性质可求出AE、O′E的长，进而可得出点O′的坐标；

（3）作点A关于x轴对称的点A′，连接A′O′交x轴于点P，此时O′P+AP′取最小值，过点O′作O′F⊥y轴，垂足为点F，过点P′作PM⊥O′F，垂足为点M，根据旋转的性质结合解直角三角形可求出点O′的坐标，由A、A′关于x轴对称可得出点A′的坐标，利用待定系数法即可求出直线A′O′的解析式，由一次函数图象上点的坐标特征可得出点P的坐标，进而可得出OP的长度，再在Rt△O′P′M中，通过解直角三角形可求出O′M、P′M的长，进而可得出此时点P′的坐标．

详解：（1）∵点A（0，4），点B（﹣2，0），∴OA=4，OB=2，∴AB==2．

在图①中，连接BB′．

由旋转可知：AB=AB′，∠BAB′=60°，∴△ABB′为等边三角形，∴BB′=AB=2．

（2）在图②中，过点O′作O′D⊥x轴，垂足为D，交AB′于点E．

∵AB′∥x轴，O′E⊥x轴，∴∠O′EA=90°=∠AOB．

由旋转可知：∠B′AO′=∠BAO，AO′=AO=4，∴△AO′E∽△ABO，==，即==，∴AE=，O′E=，∴O′D=+4，∴点O′的坐标为（+4）．

（3）作点A关于x轴对称的点A′，连接A′O′交x轴于点P，此时O′P+AP′取最小值，过点O′作O′F⊥y轴，垂足为点F，过点P′作PM⊥O′F，垂足为点M，如图3所示．

由旋转可知：AO′=AO=4，∠O′AF=240°﹣180°=60°，∴AF=AO′=2，O′F=AO′=2，∴点O′（﹣2，6）．

∵点A（0，4），∴点A′（0，﹣4）．

设直线A′O′的解析式为y=kx+b，将A′（0，﹣4）、O′（﹣2，6）代入y=kx+b，得：

，解得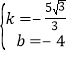：，∴直线A′O′的解析式为y=﹣x﹣4．

当y=0时，有﹣x﹣4=0，解得：x=﹣，∴点P﹣，0），∴OP=O′P′=．

在Rt△O′P′M中，∠MO′P′=60°，∠O′MP′=90°，∴O′M=O′P′=，P′M=O′P′=，∴点P′的坐标为（﹣2+，6+），即（﹣）．