��Ŀ����
��ͼ������ABCD��������EFGH��F��B�غϣ�EF��AB�ϣ���DH������14�֣�
�š���ͼ����֪��
���߶�AE=CG�� AE��CG����ֱ���ഹֱ���Ҵ�ʱ����â� ��
��
�ơ�����������EFGH��F����ʱ����ת �ȣ�ͼ2�������е����������Ƿ���Ȼ��������������ѡ������һ������֤����������������˵�����ɡ�
�ȣ�ͼ2�������е����������Ƿ���Ȼ��������������ѡ������һ������֤����������������˵�����ɡ�
�ǡ�����ͼ���е�������EFGH��BD������ÿ��1cm���ٶ�ƽ�ƣ���ƽ��ʱ��Ϊx�룬������ABCD��������EFGH�ı߳��ֱ�Ϊ5cm��1cm��
����ƽ�ƹ����У���AFH�Ƿ���Ϊ���������Σ��������x��ֵ�������ܣ�˵�����ɣ�
����ƽ�ƹ����У���AFH�Ƿ���Ϊ�ȱ������Σ��������x��ֵ�������ܣ���������ABCD��������EFGH�ı߳��ֱ�Ϊacm��bcm����a��b����ʲô��ϵʱ����AFH���Գ�Ϊ�ȱ������Σ�
�š���ͼ����֪��
���߶�AE=CG�� AE��CG����ֱ���ഹֱ���Ҵ�ʱ����â�
 ��
���ơ�����������EFGH��F����ʱ����ת
 �ȣ�ͼ2�������е����������Ƿ���Ȼ��������������ѡ������һ������֤����������������˵�����ɡ�
�ȣ�ͼ2�������е����������Ƿ���Ȼ��������������ѡ������һ������֤����������������˵�����ɡ��ǡ�����ͼ���е�������EFGH��BD������ÿ��1cm���ٶ�ƽ�ƣ���ƽ��ʱ��Ϊx�룬������ABCD��������EFGH�ı߳��ֱ�Ϊ5cm��1cm��
����ƽ�ƹ����У���AFH�Ƿ���Ϊ���������Σ��������x��ֵ�������ܣ�˵�����ɣ�
����ƽ�ƹ����У���AFH�Ƿ���Ϊ�ȱ������Σ��������x��ֵ�������ܣ���������ABCD��������EFGH�ı߳��ֱ�Ϊacm��bcm����a��b����ʲô��ϵʱ����AFH���Գ�Ϊ�ȱ������Σ�

�⣺��1����AE=CG����
��2����������ABCD��������EFGH��
���ABC=��=EBG=90�㣬
��Ϧ�=90��-��ABG����CBG=90��-��ABG��
��Ϧ�=��CBG��
����AB=BC��EB=BG��
���AEB�ա�CGB����AE=CG��
�ࣨ1���е��������۶�������
1����ABCD�߳�=5��EFGH=1ʱ����AFH�����Ϊ�ȱ������Ρ�
��ABCD�߳�Ϊa��EFGH�߳�Ϊb������AC��AC��BD�ཻ��K�㣨AC��BD���ֱƽ�֣�����֤���˰ɣ�
AK =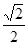 a��FK=
a��FK=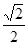 b��
b��
AF2=AK2 +FK2����AF2=a2 /2+b2/2
����AFHΪ�ȱ������Σ���ôAK=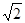 b
b
���ԣ�2b2=a2/2+b2/2
����a��b=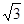 ��1
��1
���ԣ���ABCD�ı߳���EFGH�߳���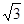 ��ʱ��AFH����Ϊ�������Ρ�
��ʱ��AFH����Ϊ�������Ρ�

��2����������ABCD��������EFGH��
���ABC=��=EBG=90�㣬
��Ϧ�=90��-��ABG����CBG=90��-��ABG��
��Ϧ�=��CBG��
����AB=BC��EB=BG��
���AEB�ա�CGB����AE=CG��
�ࣨ1���е��������۶�������
1����ABCD�߳�=5��EFGH=1ʱ����AFH�����Ϊ�ȱ������Ρ�
��ABCD�߳�Ϊa��EFGH�߳�Ϊb������AC��AC��BD�ཻ��K�㣨AC��BD���ֱƽ�֣�����֤���˰ɣ�
AK =
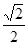 a��FK=
a��FK=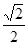 b��
b��AF2=AK2 +FK2����AF2=a2 /2+b2/2
����AFHΪ�ȱ������Σ���ôAK=
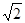 b
b���ԣ�2b2=a2/2+b2/2
����a��b=
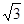 ��1
��1���ԣ���ABCD�ı߳���EFGH�߳���
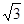 ��ʱ��AFH����Ϊ�������Ρ�
��ʱ��AFH����Ϊ�������Ρ���1������DB����֤����DHG�ա�DHE������AE=CG����ֱ�ӵó����ۣ�
��2������֤�Ϧ��͡�CBG��ȣ�����SAS��֤��AEB�ա�CBG�����ɣ�
��3���ٸ��ݵ��������ε����ʣ����ǵ������������ɣ�
�ڸ��ݵȱ������ε����ʼ��ɵõ������
��2������֤�Ϧ��͡�CBG��ȣ�����SAS��֤��AEB�ա�CBG�����ɣ�
��3���ٸ��ݵ��������ε����ʣ����ǵ������������ɣ�
�ڸ��ݵȱ������ε����ʼ��ɵõ������

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ

 ͬ����
ͬ����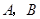 ������ׯ��
������ׯ��
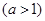 ���ּƻ��ںӰ�
���ּƻ��ںӰ�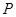 ������ˮ����������ׯ��ˮ��
������ˮ����������ׯ��ˮ��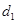 ����
����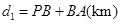 ������
������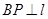 �ڵ�
�ڵ�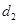 ����
����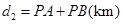 �����е�
�����е� ���
��� ����
���� ��
��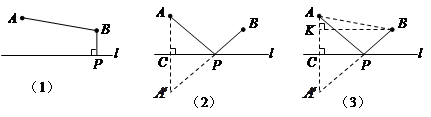
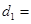 km���ú�
km���ú� ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����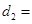 km���ú�
km���ú�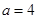 ʱ���Ƚϴ�С��
ʱ���Ƚϴ�С�� �����������������������
�����������������������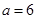 ʱ���Ƚϴ�С��
ʱ���Ƚϴ�С��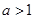 ʱ��������ȡֵ������з�����Ҫʹ����Ĺܵ����Ƚ϶̣�Ӧѡ��һ���Ƿ�������
ʱ��������ȡֵ������з�����Ҫʹ����Ĺܵ����Ƚ϶̣�Ӧѡ��һ���Ƿ�������
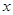 ��ĶԳƵ�
��ĶԳƵ�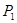 �������� ������
�������� ������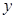 ��ĶԳƵ�
��ĶԳƵ�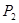 �������� ��
�������� ��