题目内容
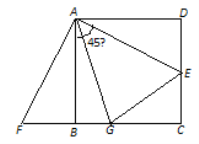
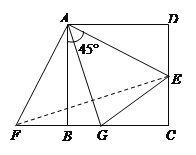
【题目】如图,已知正方形ABCD的边长是2,E是DC上一点,△ADE经顺时针旋转后与△ABF重合.
(1)指出旋转的中心和旋转的角度;
(2)如果连结EF,那么△AEF是怎样的三角形?请说明理由.
(3)已知点G在BC上,且∠GAE=45°.
① 试说明GE=DE+BG.
② 若E是DC的中点,求BG的长.
【答案】(1)旋转的中心是点A,旋转的角度是90°(2)△AEF是等腰直角三角形(3)①证明见解析② BG=![]()
【解析】试题分析:(1)根据正方形的性质得到AB=AD,∠BAD=90°,然后利用旋转的定义得到当△ADE经顺时针旋转后与△ABF重合时,可确定旋转的中心和旋转的角度;
(2)由(1)得到△ADE绕着点A逆时针旋转90°后与△ABF重合,根据旋转的性质得∠FAE=90°,AF=AE,由此可判断△AEF是等腰直角三角形;
(3)①首先得出AG是线段EF的垂直平分线,进而得出DE+GB=BF+BG=GF,即可得出答案;
②首先设GB=x,则GC=2-x,GE=1+x.在Rt△ECG中,∠C=90°,由勾股定理,得1+(2-x)2=(1+x)2,求出x即可.
试题解析:(1)∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴当△ADE经顺时针旋转后与△ABF重合时,旋转的中心是点A,旋转的角度是90°;
(2)△AEF是等腰三角形,理由:
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴△ADE绕点A顺时针旋转90°后与△ABF重合,
∴△ADE≌△ABF,
∴AE=AF,
又∵∠EAF=90°,
∴△AEF是等腰三角形;
(3)①∵ ∠GAE=45°,∠EAF=90°,
∴ AG是∠EAF的平分线,
又∵ AF=AE,
∴ AG是线段EF的垂直平分线,
∴ GE=GF.
∵ DE=BF,
∴ DE+GB=BF+BG=GF,
∴ GE=DE+BG;
② ∵ E是DC的中点,
∴ DE=EC=FB=1,
设GB=x,则GC=2-x,GE=1+x,
在Rt△ECG中,∠C=90°,由勾股定理,得
1+(2-x)2=(1+x)2,
解这个方程,得x=![]() ,
,
即:BG=![]() .
.