Question

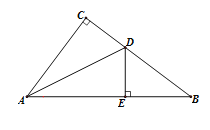
【题目】如图，在△ABC中，∠C=90°，AD平分∠BAC交BC于D点，DE⊥AB于E，当AC=6，BC=8时，求DE的长．

Answer 1

【答案】3

【解析】根据全等三角形的判定和性质、勾股定理即可对本题求解，

解：∵∠C=90°，DE⊥AB于E，

∴∠ACD =∠AED=90°，

∵AD平分∠BAC交BC于D点，

∴∠CAD =∠EAD，

在Rt△ACD和Rt△AED中，

，

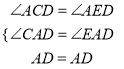∴△ACD≌△AED（AAS），

∴ AE=AC=6 ，DE=CD ，

∵BC=8，由勾股定理得，

∴AB2=AC2+BC2=62+82=100，

∴AB=10，

∴BE=AB-AE=4，

设DE=CD=x ，则BD =8-x，

在Rt△DEB中，由勾股定理得x2+42=(8-x)2 ，

解得 x = 3，

∴DE=3.