Question

【题目】已知：如图，在矩形ABCD中，AC是对角线．点P为矩形外一点且满足AP=PC，AP⊥PC．PC交AD于点N，连接DP，过点P作PM⊥PD交AD于M．

（1）若AP=，AB=BC，求矩形ABCD的面积；

（2）若CD=PM，求证：AC=AP+PN．

Answer 1

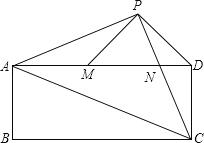
【答案】（1）3（2）AC=AP+PN

【解析】（1）∵AP⊥CP且AP＝CP

∴△APC为等腰直角三角形

∵AP＝

∴AC＝.................1分

∵AB＝BC

∴设AB＝x，BC＝3x

∴在Rt△ABC中

x2+(3x)2=10

10x2=10

x=1.................3分

∴.................4分

（2）延长AP，CD交于Q

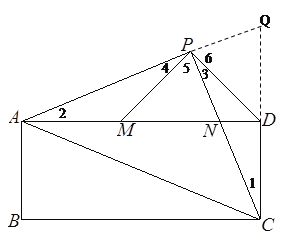
∵∠1+∠CND=∠2+∠PNA=900

且∠CND=∠ANP

∴∠1=∠2

又∠3+∠5=∠4+∠5=900

∴∠3=∠4

又∵AP＝CP

∴△APM≌△CPD

∴DP＝PM

又∵CD＝PM

∴CD＝PD

∴∠1＝∠3

∠1+∠Q＝∠3+∠6＝90°

∵∠1＝∠3

∴∠Q=∠6

∴DQ=DP=CD

∴D为CQ中点

又∵AD⊥CQ

∴AC＝AQ＝AP+PQ

又∵∠1＝∠2

∠APN＝∠CPQ＝900

AP=CP ∴△APN≌△CPQ

∴PQ＝PN

∴AC＝AP+PQ＝AP+PN.................10分

（1）由已知条件知△APC为等腰直角三角形，即可求得AC的长，再利用勾股定理求得AB，BC的长，从而求得矩形ABCD的面积

（2）延长AP，CD交于Q,通过角之间的等量关系，求得△APN≌△CPQ，得出PQ＝PN，从而求得结论