题目内容
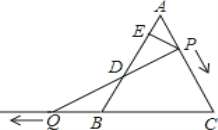
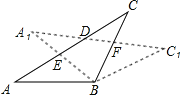
【题目】如图,在△ABC.中,AB=BC,将△ABC绕点B顺时针旋转α度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于点D、F,下列结论:①∠CDF=α,②A1E=CF,③DF=FC,④A1F=CE.其中正确的是 (写出正确结论的序号).

【答案】①②④
【解析】①两个不同的三角形中有两个角相等,那么第三个角也相等;
②根据两边及一边的对角对应相等的两三角形不一定全等,进而得不到△ADE与△CDF全等,可得结论A1E与CF不一定全等;
③∠CDF=α,而∠C与顺时针旋转的度数不一定相等,所以DF与FC不一定相等;
④用角角边证明△A1BF≌△CBE后可得A1F=CE.
解:①∠C=∠C1(旋转后所得三角形与原三角形完全相等)
又∵∠DFC=∠BFC1(对顶角相等)
∴∠CDF=∠C1BF=α,故结论①正确;
②∵AB=BC,
∴∠A=∠C,
∴∠A1=∠C,A1B=CB,∠A1BF=∠CBE,
∴△A1BF≌△CBE(ASA),
∴BF=BE,
∴A1B﹣BE=BC﹣BF,
∴A1E=CF,故②正确;
③在三角形DFC中,∠C与∠CDF=α度不一定相等,所以DF与FC不一定相等,
故结论③不一定正确;
④∠A1=∠C,BC=A1B,∠A1BF=∠CBE
∴△A1BF≌△CBE(ASA)
那么A1F=CE.
故结论④正确.
故答案为:①②④.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目