Question

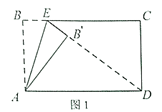
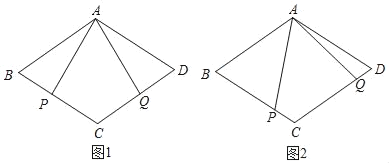
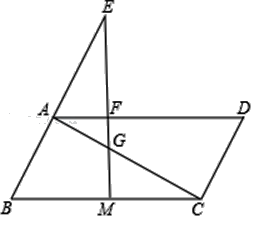
【题目】已知矩形纸片中，，，点为边上的动点（点不与点、重合），如图1所示，沿折痕翻折得到，设．

（1）当、、在同一直线上时，求的值；

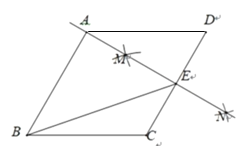
（2）如图2，点在边上，沿再次折叠纸片，使点的对应点在直线上，

①求的最小值；

②点能否落在边上？若能，求出的值，若不能，试说明理由．

Answer 1

【答案】（1）2 （2）① ②见解析

【解析】

（1）由折叠的性质可知∠BEA＝∠B′EA，再根据矩形的性质可得∠B′EA＝∠EAD，即可得ED＝AD＝10，根据勾股股定理求出CE的长度，即可求出BE的长度．

（2）①先证明△ABE∽△ECF，于是，可求得DF＝，再根据二次函数的性质求解即可；②根据勾股定理可得，再根据根的判别式来确定方程的根的情况，从而判断点能否落在边上．

（1）由折叠可知，∠BEA＝∠B′EA，

又∵矩形ABCD中，BC//AD，

∴∠BEA＝∠EAD，

∴∠B′EA＝∠EAD，

∴ED＝AD＝10，

∵CD＝AB＝6，

根据勾股定理求得CE＝8，

∴BE＝BC－CE＝2；

（2）①根据两次折叠可求证得∠AEF＝90度，从而证得△ABE∽△ECF，于是，

∴，CF＝，

∴DF＝＝

∴当m=5时，DF的最小值为.

②不能．理由是：

若点C′落在边AD上，由（1）知A C′＝E C′，

根据折叠可知：BE＝B′E＝m， E C′＝EC＝10－m，

∴A C′＝10－m，B′C′＝E C′－B′E＝10－m－m=10-2m，A C′＝6，

在Rt△A B′C′中，根据勾股定理得：.

化简得：

∴

∴原方程没有实数解，

∴点C′不能落在边AD上