Question

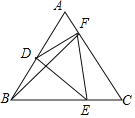
【题目】已知△ABC是等边三角形，AB＝6，点D，E，F分别在边AB，BC，AC上，BD：BE＝2：3，DE同时平分∠BEF和∠BDF，则BD的长为___．

Answer 1

【答案】

【解析】

根据角平分线的定义得到∠BDE＝∠FDE，∠BED＝∠FED，根据全等三角形的性质得到∠DBE＝∠DFE，BD＝DF，BE＝EF，由等边三角形的性质得到∠A＝∠ABC＝∠C＝60°，求得∠DFE＝60°，根据相似三角形的性质即可得到结论．

解：如图，∵DE同时平分∠BEF和∠BDF，

∴∠BDE＝∠FDE，∠BED＝∠FED，

在△BDE与△FDE中，，

∴△BDE≌△FDE(ASA)，

∴∠DBE＝∠DFE，BD＝DF，BE＝EF，

∵△ABC是等边三角形，

∴∠A＝∠ABC＝∠C＝60°，

∴∠DFE＝60°，

∴∠ADF＝∠AFD＝∠AFD+∠CFE＝120°，

∴∠ADF＝∠CFE，

∴△ADF∽△CFE，

∴，

∵BD：BE＝2：3，

∴设BD＝DF＝2x，BE＝EF＝3x，

∴AD＝6﹣2x，CE＝6﹣3x，

∴＝＝，

∴CF＝9﹣3x，AF＝4﹣2x，

∵AF+CF＝6，

∴9﹣3x+4﹣2x＝6，

∴x＝，

∴BD＝2x＝．

故答案为：．