题目内容
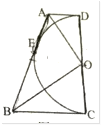
【题目】如图，AC是
的直径，AB与相切于点A，四边形ABCD是平行四边形，BC交于点E．
判断直线CD与的位置关系，并说明理由；
若的半径为5cm，弦CE的长为8cm，求AB的长．
【答案】（1）直线CD与
相切，证明详见解析；（2）
．
【解析】
（1）根据题意，易得∠BAC=90°，又由四边形ABCD是平行四边形，结合平行四边形的性质AB∥CD，可得∠BAC=∠DCA=90°，故直线CD与⊙O相切，
（2）连接AE，易得△CAE∽△CBA，进而可得
，在Rt△AEC中，由勾股定理可得AE的值，代入关系式，可得答案．
解：
直线CD与
相切，
理由：
是的直径，AB与相切于点A，
，
又
四边形ABCD是平行四边形，
，
，
直线CD与相切；
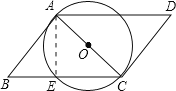
连接AE，
为圆的直径，
，
与相切于点A，
，
，
，
又
，
∽
，
，
又
，
，
根据勾股定理可得，
，
代入关系式
得，
，
解得
．
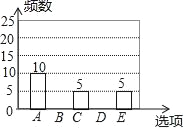
【题目】随着移动终端设备的升级换代，手机已经成为我们生活中不可缺少的一部分，为了解中学生在假期使用手机的情况（选项：A．和同学亲友聊天；B．学习；C．购物；D．游戏；E．其它），端午节后某中学在全校范围内随机抽取了若干名学生进行调查，得到如下图表（部分信息未给出）：根据以上信息解答下列问题：
(1)这次被调查的学生有多少人？
(2)求表中m，n，p的值，并补全条形统计图.
(3)若该中学约有800名学生，估计全校学生中利用手机购物或玩游戏的共有多少人？并根据以上调查结果，就中学生如何合理使用手机给出你的一条建议.
选项 | 频数 | 频率 |
A | 10 | m |
B | n | 0.2 |
C | 5 | 0.1 |
D | p | 0.4 |
E | 5 | 0.1 |
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表所示：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知，下列说法中，错误的是（ ）
A. 抛物线于x轴的一个交点坐标为（﹣2，0）
B. 抛物线与y轴的交点坐标为（0，6）
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的
