题目内容
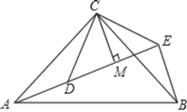
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 以
以![]() 的速度移动,设运动的时间为
的速度移动,设运动的时间为![]() 秒.
秒.
(1)求![]() 边的长;
边的长;
(2)当![]() 为直角三角形时,求
为直角三角形时,求![]() 的值;
的值;
(3)当![]() 为轴对称图形时,求
为轴对称图形时,求![]() 的值.
的值.

【答案】(1)4cm;(2)当![]() 为直角三角形时,t=4或
为直角三角形时,t=4或![]() ;(3)当
;(3)当![]() 为轴对称图形时,t=8或5或
为轴对称图形时,t=8或5或![]()
【解析】
(1)利用勾股定理即可求出结论;
(2)由题意可得:BC=tcm,∠B≠90°,然后根据直角三角形直角的情况分类讨论,利用勾股定理等知识即可解答;
(3)当![]() 为轴对称图形时,△ABP必是等腰三角形,然后根据等腰三角形腰的情况分类讨论,分别画出对应的图形,根据三线合一、勾股定理等知识即可解答.
为轴对称图形时,△ABP必是等腰三角形,然后根据等腰三角形腰的情况分类讨论,分别画出对应的图形,根据三线合一、勾股定理等知识即可解答.
解:(1)∵在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴BC=![]()
(2)由题意可得:BC=tcm,∠B≠90°
当∠APB=90°时,易知点P与点C重合
∴BP = BC
即t=4;
当∠PAB=90°时,如下图所示
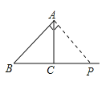
∴CP=BP-BC=(t-4)cm
∵AC2+CP2=AP2=BP2-AB2
∴32+(t-4)2=t2-52
解得:t=![]()
综上:当![]() 为直角三角形时,t=4或
为直角三角形时,t=4或![]() ;
;
(3)当![]() 为轴对称图形时,△ABP必是等腰三角形
为轴对称图形时,△ABP必是等腰三角形
当AB=AP时,如下图所示
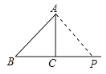
∵AC⊥BC
∴BP=2BC
即t=2×4=8
当AB=BP时,如下图所示

∴t=5;
当AP=BP时,如下图所示
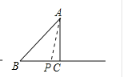
则CP=BC-BP=(4-t)cm,AP=BP=t
在Rt△APC中,![]()
即![]()
解得:t=![]()
综上:当![]() 为轴对称图形时,t=8或5或
为轴对称图形时,t=8或5或![]() .
.

练习册系列答案
相关题目