题目内容
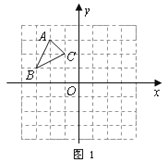
【题目】如图1,已知正方形![]() 的顶点
的顶点![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,边
轴上,边![]() 交
交![]() 轴的正半轴于点
轴的正半轴于点![]() .
.


(1)若![]() ,且
,且![]() ,求
,求![]() 点的坐标;
点的坐标;
(2)在(l)的条件下,若![]() ,求
,求![]() 点的坐标;
点的坐标;
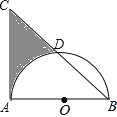
(3)如图2,连结![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 是
是![]() 点上方
点上方![]() 轴上一动点,以
轴上一动点,以![]() 、
、![]() 为边作
为边作![]() ,使
,使![]() 点恰好落在
点恰好落在![]() 边上,试探讨
边上,试探讨![]() ,
,![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,见解析
,见解析
【解析】
(1)根据a值和点A的坐标![]() 可求得结果;
可求得结果;
(2)作![]() 于
于![]() ,再作
,再作![]() 于
于![]() ,连
,连![]() ,证明
,证明![]() ,得到
,得到![]() ,再根据
,再根据![]() 得到
得到![]() ,EN=1,设
,EN=1,设![]() ,最后利用勾股定理求出m值即可;
,最后利用勾股定理求出m值即可;
(3)过F作FM⊥AB于M,FN⊥AD于N,证明Rt△BFM≌Rt△GFN,得到BF=GF,再证明△BAF≌△DAF,得到BF=DF,再通过勾股定理以及等量代换得到![]() ,
,![]() 与
与![]() 的数量关系.
的数量关系.
解:(1)∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() 点的坐标为
点的坐标为![]() ;
;
(2)解:作![]() 于
于![]() ,再作
,再作![]() 于
于![]() ,连
,连![]() ,
,
则![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中, ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,EN=1,
,EN=1,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
设![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
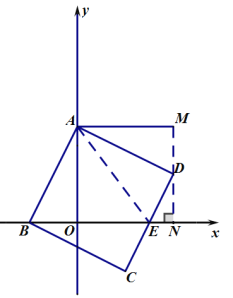
(3)∵平行四边形AFGH,
∴GH=AF,GF∥OA,即GF⊥BF,
过F作FM⊥AB于M,FN⊥AD于N,
∵AF平分∠BAD,
∴FM=FN,
又∵∠BAG=∠BFG=90°,
∴∠ABF+∠AGF=180°,
又∵∠DGF+∠AGF=180°,
∴∠MBF=∠NGF,
∴Rt△BFM≌Rt△GFN,
∴BF=GF,
又∵∠BAF=∠DAF=45°,AB=AD,AF=AF,
∴△BAF≌△DAF,
∴BF=DF,
∴GF=DF,
又∵FN⊥DG,
∴DN2=(![]() DG)2,
DG)2,
∴DN2=![]() DG2,
DG2,
在Rt△AFN中,∠FAN=45°,
∴AN=FN,
∴AF2=AN2+FN2=2FN2,
∴FN2=![]() AF2,
AF2,
在Rt△DFN中,DF2=DN2+FN2,
∴BF2=![]() DG2+
DG2+![]() AF2,
AF2,
∴4BF2=DG2+2AF2,
又∵AF=HG,
∴4BF2=DG2+2HG2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目