题目内容
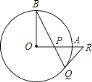
【题目】如图,![]() 和
和![]() 是
是![]() 的半径,并且
的半径,并且![]() ,
,![]() 是
是![]() 上任一点,
上任一点,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,过点
,过点![]() 的
的![]() 的切线交
的切线交![]() 延长线于点
延长线于点![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,试求
,试求![]() 的长.
的长.
【答案】(1)证明见解析; (2)![]() .
.
【解析】
(1)要证明RP=RQ,需要证明∠PQR=∠RPQ,连接OQ,则∠OQR=90°;根据OB=OQ,得∠B=∠OQB,再根据等角的余角相等即可证明;
(2)延长AO交圆于点C,首先根据勾股定理求得BP的长,再根据相交弦定理求得QP的长即可.
(1)证法一:
连接OQ.
∵RQ是⊙O的切线,∴∠OQB+∠BQR=90°.
∵OA⊥OB,∴∠OPB+∠B=90°.
又∵OB=OQ,∴∠OQB=∠B,∴∠PQR=∠BPO=∠RPQ,∴RP=RQ.
证法二:
作直径BC,连接CQ.
∵BC是⊙O的直径,∴∠B+∠C=90°.
∵OA⊥OB,∴∠B+∠BPO=90°,∴∠C=∠BPO.
又∵∠BPO=∠RPQ,∴∠C=∠RPQ.
又∵RQ为⊙O的切线,∴∠PQR=∠C,∴∠PQR=∠RPQ,∴RP=RQ.
(2)解法一:
作直径AC.
∵OP=PA=1,∴PC=3.
由勾股定理,得:BP=![]() =
=![]() .
.
由相交弦定理,得:PQPB=PAPC,即PQ×![]() =1×3,∴PQ=
=1×3,∴PQ=![]() .
.
解法二:
作直径AE,过R作RF⊥BQ,垂足为F,设RQ=RP=x;
由切割线定理,得:x2=(x﹣1)(x+3)
解得:x=![]() .
.
∵∠BOP=∠RFP=90°,∠BPO=∠RPF,∴△BPO∽△RPF,∴![]() ,∴PF=
,∴PF=![]() ,由等腰三角形性质得:PQ=2PF=
,由等腰三角形性质得:PQ=2PF=![]() .
.

练习册系列答案
相关题目
【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?