Question

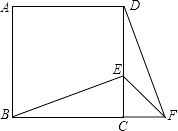
【题目】在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，E，F分别是AC，BC边上一点．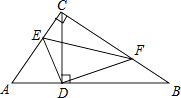
（1）求证： ；
（2）若CE= AC，BF= BC，求∠EDF的度数．

Answer 1

【答案】
（1）解：∵CD⊥AB，

∴∠A+∠ACD=90°

又∵∠A+∠B=90°

∴∠B=∠ACD

∴Rt△ADC∽Rt△CDB

∴

（2）解：∵ = = ，

又∵∠ACD=∠B，

∴△CED∽△BFD；

∴∠CDE=∠BDF；

∴∠EDF=∠EDC+∠CDF=∠BDF+∠CDF=∠CDB=90°

【解析】（1）证相关线段所在的三角形相似即可，即证Rt△ADC∽Rt△CDB；（2）易证得CE：BF=AC：BC，联立（1）的结论，即可得出CE：BF=CD：BD，由此易证得△CED∽△BFD，即可得出∠CDE=∠BDF，由于∠BDF和∠CDF互余，则∠EDC和∠CDF也互余，由此可求得∠EDF的度数．
【考点精析】通过灵活运用相似三角形的判定与性质，掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方即可以解答此题．