题目内容
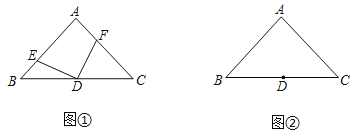
【题目】如图,平行四边形![]() 中,
中,![]() 平分
平分![]() 交
交![]() 边于
边于![]() ,
,![]() 交
交![]() 边于
边于![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,![]() ,则平行四边形
,则平行四边形![]() 的面积为________.
的面积为________.

【答案】21
【解析】
注意到AE既是角平分线又是EF的垂线,于是根据三线合一构造出等腰三角形,即双向延长EF分别交AB、AD于M、N,则AM=AN.又由AD∥BC可推出BA=BE,由BC=7,DF=3,EC=CF可求出CE=CF=2,结合tan∠AEB=3,算出AE、ME的长度,从而求出△AMN的面积,接着利用相似三角形的面积之比等于相似比的平方这一性质可分别算出△BME、△CEF、△DFN的面积,再用割补法算出平行四边形ABCD的面积.
如图,延长EF交AD于N,延长FE交AB于点M,

∵∠BAE=∠EAD,
∴∠BAE=∠AEB,
∴AB=BE,
设CF=x,
∵CF=EC,DF=3,
∴EC=x,CD=AB=BE=3+x,
∵BC=BE+CE=7,
∴x=2,AB=BE=CD=5,
显然△BEM∽△CEF∽△DNF,
∴BM=BE=5,DN=DF=3,
∴AM=AN=10,
∵AE⊥EF,
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
故答案为:21.

练习册系列答案
相关题目