Question

【题目】如图，为的直径延长线上的一点，与相切，切点为，点是上一点，连接．已知．下列结论：

与相切；四边形是菱形；；．

其中正确的个数为（ ）

A. 个 B. 个 C. 个 D. 个

Answer 1

【答案】A

【解析】

（1）利用切线的性质得出∠PCO=90°，进而得出△PCO≌△PDO（SSS），即可得出∠PCO=∠PDO=90°，得出答案即可；（2）利用（1）所求得出：∠CPB=∠BPD，进而求出△CPB≌△DPB（SAS），即可得出答案；（3）利用全等三角形的判定得出△PCO≌△BCA（ASA），进而得出CO=12PO=12AB；（4）利用四边形PCBD是菱形，∠CPO=30°，则DP=DB，则∠DPB=∠DBP=30°，求出即可．

(1)连接CO，DO，

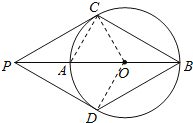
∵PC与⊙O相切，切点为C，

∴

在△PCO和△PDO中，

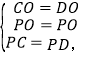
∴△PCO≌△PDO(SSS)，

∴ ∴PD与⊙O相切，

故(1)正确；

(2)由(1)得：∠CPB=∠BPD，

在△CPB和△DPB中，

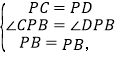
∴△CPB≌△DPB(SAS)，

∴BC=BD，

∴PC=PD=BC=BD，

∴四边形PCBD是菱形，

故(2)正确；

(3)连接AC，

∵PC=CB，

∴∠CPB=∠CBP，

∵AB是⊙O直径，

∴

在△PCO和△BCA中，

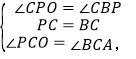
∴△PCO≌△BCA(ASA)，

∴AC=CO，

∴AC=CO=AO，

∴

∴

∴

∴PO=AB，

故(3)正确；

(4)∵四边形PCBD是菱形,

∴DP=DB,则

∴故(4)正确；

正确个数有4个，

故选：A.