题目内容
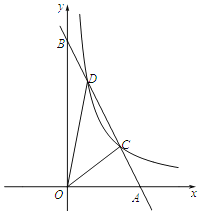
【题目】如图,已知直线y=﹣2x+4与x轴交于点A,与y轴交于点B,与双曲线y=![]() (x>0)交于C、D两点,且∠AOC=∠ADO,则k的值为_____.
(x>0)交于C、D两点,且∠AOC=∠ADO,则k的值为_____.
【答案】![]()
【解析】
先利用面积判断出BD=AC,再判断出△AOC∽△ADO,进而建立方程求出AC=BD,再判断出△ACE∽△ABO,进而求出CE,OE,即可得出结论.
解:由已知得OA=2,OB=4,根据勾股定理得出,AB=2![]() ,
,
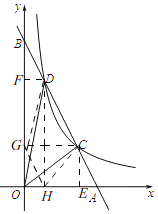
如图,过点C作CE⊥x轴于E,作CG⊥y轴G,过点D作DH⊥x轴于H,作DF⊥y轴于F,连接GH,GD,CH,
∵点C,D是反比例图象上的点,
∴S矩形FDHO=S矩形GCEO,
∴![]() S矩形FDHO=
S矩形FDHO=![]() S矩形GDEO.
S矩形GDEO.
∴S△DGH=S△GHC.
∴点C,D到GH的距离相等.
∴CD∥GH.
∴四边形BDHG和四边形GHAC都是平行四边形.
∴BD=GH,GH=CA.
即BD=AC;
设AC=BD=m,
∵∠AOC=∠ADO,
CAO=∠DAO,
∴△AOC∽△ADO,
∴![]() ,
,
∴AO2=ACAD,
∴22=m(2![]() ﹣m),
﹣m),
∴m=![]() ±1(舍去
±1(舍去![]() +1),
+1),
过点C作CE⊥x轴于点E,
∴△ACE∽△ABO,
∴![]() ,
,
∴![]() ,
,
∴AE=![]() ,CE=
,CE=![]() ,
,
∴OE=OA﹣AE=2﹣![]() =
=![]() OE=
OE=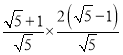 =
=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目