题目内容
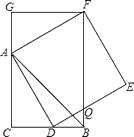
【题目】如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB,求∠APB的度数.
【答案】解:∵△PCD是等边三角形,
∴∠PCD=60°,
∴∠ACP=120°,
∵△ACP∽△PDB,
∴∠APC=∠B,又∠A=∠A,
∴△ACP∽△ABP,
∴∠APB=∠ACP=120°
【解析】由等边三角形的三个角都是60°易得∠ACP=120°,又由所给△ACP∽△PDB可证△ACP∽△ABP,最后可得∠APB=∠ACP=120°
【考点精析】通过灵活运用相似三角形的判定与性质,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.

练习册系列答案
相关题目