Question

【题目】在平面直角坐标系中，已知平行四边形ABCD的点A（0，﹣2）、点B（3m，4m+1）（m≠﹣1），点C（6，2），则对角线BD的最小值是（　　）

A. 3 B. 2 C. 5 D. 6

Answer 1

【答案】D

【解析】分析：先根据B（3m，4m+1），可知B在直线y=x+1上，所以当BD⊥直线y=x+1时，BD最小，找一等量关系列关于m的方程，作辅助线：过B作BH⊥x轴于H，则BH=4m+1，利用三角形相似得BH2=EHFH，列等式求m的值，得BD的长即可．

详解：如图,

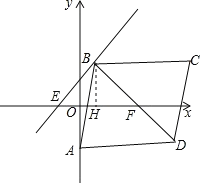
∵点B(3m,4m+1)，

∴令，

∴y=x+1，

∴B在直线y=x+1上，

∴当BD⊥直线y=x+1时，BD最小，

过B作BH⊥x轴于H，则BH=4m+1，

∵BE在直线y=x+1上，且点E在x轴上，

∴E(,0),G(0,1)

∵F是AC的中点

∵A(0,2),点C(6,2)，

∴F(3,0)

在Rt△BEF中，

∵BH2=EHFH，

∴(4m+1)2=(3m+)(33m)，

解得：m1= (舍),m2=，

∴B(,)，

∴BD=2BF=2×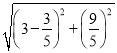=6，

则对角线BD的最小值是6；

故答案为：6.