Question

【题目】在如图所示的正方形网格中，△ABC的顶点均在格点上，请在所给的平面直角坐标系中按要求作图并完成填空：

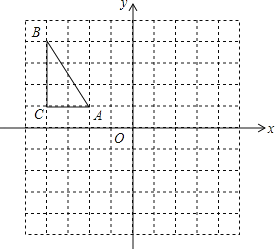
（1）作出△ABC关于原点O成中心对称的△A1B1C1，写出点A1的坐标_______.

（2）作出△A1B1C1绕点O逆时针旋转90°的△A2B2C2，写出线段C1C2的长度_____．

Answer 1

【答案】（1）作图见解析；（2，﹣1）；（2）作图见解析；．

【解析】

（1）根据关于原点对称的点的特征得出A1、B1、C1的坐标，顺次连接即可得△A1B1C1；

（2）连接OA1、OB1、OC1，利用网格特点和旋转的性质得出点A1、B1、C1的对应点A2、B2、C2，顺次连接即可得到△A2B2C2，利用勾股定理求出C1C2的长即可.

（1）如图，∵点A（-2，1），B（-4，4），C（-4，1），

∴点A、B、C关于原点对称的点的坐标为：A1（2，-1），B1（4，-4），C1（4，-1），

顺次连接A1、B1、C1，△A1B1C1即为所求，

点A1的坐标为（2，﹣1）；

（2）如图，连接OA1、OB1、OC1，

作OA2⊥OA1，OB2⊥OB1，OC2⊥OC1，使OA1=OA2，OB1=OB2，OC1=OC2，

顺次连接A2、B2、C2，△A2B2C2即为所求，

线段C1C2的长度为＝．