Question

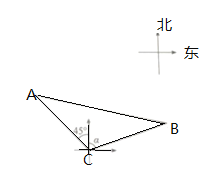
【题目】如图，梯形ABCD中，AB∥CD，∠A＝90°，E在AD上，且CE平分∠BCD，BE平分∠ABC，则下列关系式中成立的有（　　）

①，②，③，④CE2＝CDBC．

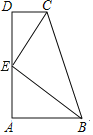
A.2个B.3个C.4个D.5个

Answer 1

【答案】A

【解析】

如图，作辅助线；首先证明∠BEC＝90°；运用勾股定理证明CD＝CF，BA＝BF；根据两角相等证明：△CDE∽△EAB和△ECF∽△BCE，列比例式进一步判断即可．

如图，过点E作EF⊥BC于点F；

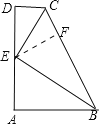
∵CD∥AB，CE平分∠BCD，BE平分∠ABC，

∴∠DCE＝∠FCE（设为α），∠ABE＝∠FBE（设为β），

且2α+2β＝180°，

∴α+β＝90°，∠BEC＝180°﹣90°＝90°；

∵∠A＝90°，DC∥AB，

∴∠D＝90°；而CE平分∠BCD，BE平分∠ABC，

∴ED＝EF，EA＝EF；

∴ED＝EF＝EA，

由勾股定理得：CD＝CF，BA＝BF；

∵∠D＝∠A，∠DCE＝∠AEB，

∴△CDE∽△EAB，

∴，,

∵四边形ABCD是梯形，

∴AD与BC不平行，

∴∠DEC≠∠ECF＝∠DCE，

∴DE≠CD，

∴①②不正确，③正确；

∵∠EFC＝∠CEB＝90°，∠ECF＝∠ECB，

∴△ECF∽△BCE，

∴,

∴CE2＝BCCF＝CDBC，

∴④正确，

故选：A．