Question

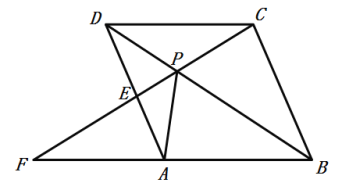
【题目】如图，点P是菱形ABCD的对角线BD上一点，连接CP并延长，交AD于E，交BA的延长线于点F.

（1）求证：.

（2）如果，求线段PC的长.

Answer 1

【答案】（1）证明见解析；（2）

【解析】

（1）根据菱形的对角线平分一组对角可得∠BDC=∠BDA，然后利用“边角边”证明△APD和△CPD全等，然后根据全等三角形对应角相等证明即可

（2）利用两组角对应相等则两三角形相似，证明△APE与△FPA相似；根据相似三角形的对应边成比例及全等三角形的对应边相等即可得到结论．

（1）在菱形ABCD中，AD=CD，∠BDC=∠BDA，

在△APD和△CPD中，∵，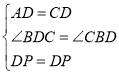

∴△APD≌△CPD（SAS），∴∠DCP=∠DAP；

（2）∵△APD≌△CPD，∴∠DAP=∠DCP．

∵CD∥AB，∴∠DCF=∠DAP=∠CFB，

又∵∠FPA=∠FPA，∴△APE∽△FPA，∴，∴PA2=PEPF．

∵△APD≌△CPD，∴PA=PC，∴PC2=PEPF．

∵PE=3，EF=5，∴PF=8，∴PC=．