Question

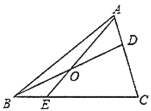
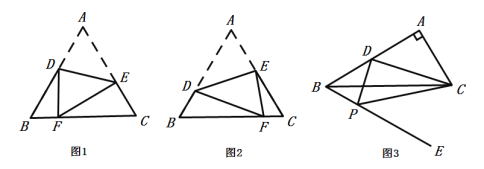
【题目】（1）如图1，△ABC为等边三角形，点D、E分别为边AB、AC上的一点，将图形沿线段DE所在的直线翻折，使点A落在BC边上的点F处求证：；

（2）如图2，按图1的翻折方式，若等边△ABC的边长为4，当时，求的值；

（3）如图3，在中，，点D是AB边上的中点，在BC的下方作射线BE，使得，点P是射线BE上一个动点，当，求BP的长.

Answer 1

【答案】（1）见解析；（2）；（3）2或6

【解析】

（1）根据三角形外角的性质证明∠BDF=∠EFC，从而可得△BDF∽△CFE，根据相似三角形对应边成比例即可得出结论；

（2）过D作DH⊥BC．设BF=x，则CF=4-x．设EF=2a，则DF=3a，AE=2a，BD=4-AD=4-3a，CE=4-AE=4-2a，由相似三角形对应边成比例，即可得出x、a的值，从而求得BD、DF、DH的长，根据正弦的定义即可得出结论；

（3）解Rt△ABC得到BC、AB、BD的长．过C作CF⊥BC，交BE于F，解Rt△BCF，得到CF、BF的长．通过证明△DBPΔPFC，由相似三角形对应边成比例即可得出结论．

（1），

又，

，

．

又，

，

，

即．

（2）过D作．

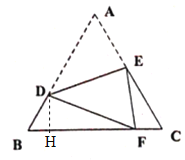
设，则．

设，则，AE=2a，

，

．

由（1）知，

，

即，

，

，

，

．

，

，

．

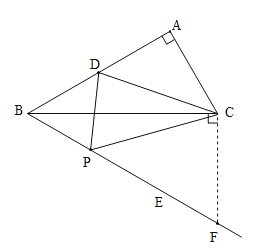
（3）∵，

∴，

，

∴．

过C作，交BE于F．

∵∠CBF=30°，

∴CF=BC=，

∴CF=4，∴BF=2CF=8．

∵，

．

∴，

又，

∴，

∴，即，

∴或6．