题目内容

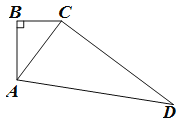
【题目】如图，四边形ABCD中，AC=5，AB=4，CD=12，AD=13，∠B=90°．

（1）求BC边的长；

（2）求四边形ABCD的面积．

【答案】（1）3；（2）36．

【解析】

（1）先根据勾股定理求出BC的长度；
（2）根据勾股定理的逆定理判断出△ACD是直角三角形，四边形ABCD的面积等于△ABC和△ACD的面积和，再利用三角形的面积公式求解即可．

解：（1）∵∠ABC=90°，AC=5，AB=4
∴BC= ，

（2）在△ACD中，AC2+CD2= 52+122=169

AD2 =132=169，

∴AC2+CD2= AD2,
∴△ACD是直角三角形，
∴∠ACD=90°；

由图形可知：S四边形ABCD=S△ABC+S△ACD= ABBC+ ACCD，
= ×3×4+ ×5×12，
=36．

练习册系列答案
相关题目

【题目】如图，的直径为，弦为，、分别是的平分线与，的交点，为延长线上一点，且．

求、的长；

试判断直线与的位置关系，并说明理由．

【题目】如图，已知一次函数y＝mx＋3的图象经过点A(2，6)，B(n，－3)．求：

(1)m，n的值；

(2)△OAB的面积．

【题目】如图，等腰△ABC，点D、E、F分别在BC、AB、AC上，且∠BAC=∠ADE=∠ADF=60°．

（1）在图中找出与∠DAC相等的角，并加以证明；

（2）若AB=6，BE=m，求：AF（用含m的式子表示）．

【题目】已知：RT△ABC与RT△DEF中，∠ACB＝∠EDF＝90°，∠DEF＝45°，EF＝8cm，AC＝16cm，BC＝12cm．现将RT△ABC和RT△DEF按图1的方式摆放，使点C与点E重合，点B、C（E）、F在同一条直线上，并按如下方式运动．

运动一：如图2，△ABC从图1的位置出发，以1cm/s的速度沿EF方向向右匀速运动，DE与AC相交于点Q，当点Q与点D重合时暂停运动；

运动二：在运动一的基础上，如图3，RT△ABC绕着点C顺时针旋转，CA与DF交于点Q，CB与DE交于点P，此时点Q在DF上匀速运动，速度为cm/s，当QC⊥DF时暂停旋转；

运动三：在运动二的基础上，如图4，RT△ABC以1cm/s的速度沿EF向终点F匀速运动，直到点C与点F重合时为止．

设运动时间为t（s），中间的暂停不计时，

解答下列问题

（1）在RT△ABC从运动一到最后运动三结束时，整个过程共耗时　 　s；

（2）在整个运动过程中，设RT△ABC与RT△DEF的重叠部分的面积为S（cm2），求S与t之间的函数关系式，并直接写出自变量t的取值范围；

（3）在整个运动过程中，是否存在某一时刻，点Q正好在线段AB的中垂线上，若存在，求出此时t的值；若不存在，请说明理由．

【题目】已知△．

（1）在图中用直尺和圆规作出的平分线和边的垂直平分线交于点（保留作图痕迹，不写作法）．

（2）在（1）的条件下，若点、分别是边和上的点，且，连接求证：；

（3）如图，在（1）的条件下，点、分别是、边上的点，且△的周长等于边的长，试探究与的数量关系，并说明理由．

【题目】如图所示，在距树米的地面上平放一面镜子，人退后到距镜子米的处，在镜子里恰巧看见树顶，若人眼距地面米．

求树高；

和是位似图形吗？若是，请指出位似中心；若不是，请说明理由．

【题目】小张去文具店购买作业本，作业本有大、小两种规格，大本作业本的单价比小本作业本贵0.3元，已知用8元购买大本作业本的数量与用5元购买小本作业本的数量相同．

（1）求大本作业本与小本作业本每本各多少元？

（2）因作业需要，小张要再购买一些作业本，购买小本作业本的数量是大本作业本数量的2倍，总费用不超过15元．则大本作业本最多能购买多少本？

【题目】阅读理解

在平面直角坐标系xoy中，两条直线l1：y=k1x+b1（k1≠0），l2：y=k2x+b2（k2≠0），①当l1∥l2时，k1=k2，且b1≠b2；②当l1⊥l2时，k1·k2=－1．

类比应用

（1）已知直线l：y=2x－1，若直线l1：y=k1x+b1与直线l平行，且经过点A（－2，1），试求直线l1的表达式；

拓展提升

（2）如图，在平面直角坐标系xoy中，△ABC的顶点坐标分别为：A（0，2），B（4，0），C（－1，－1），试求出AB边上的高CD所在直线的表达式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网