题目内容
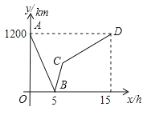
【题目】一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，慢车的速度是快车速度的
，两车同时出发．设慢车行驶的时间为x（h），两车之间的距离为y（km），图中的折线表示y与x之间的函数关系．
根据图象解决以下问题：
（1）甲、乙两地之间的距离为 km；D点的坐标为 ；
（2）求线段BC的函数关系式，并写出自变量x的取值范围；
（3）若第二列快车从乙地出发驶往甲地，速度与第一列快车相同．在第一列快车与慢车相遇30分钟后，第二列快车追上慢车．求第二列快车比第一列快车晚出发多少小时？
【答案】（1）1200，D（15，1200）；（2）y=240x-1200（5≤x≤7.5）；（3）2.75小时．
【解析】
（1）由题意直接根据图象即可得出答案；
（2）设慢车速度为a千米/小时，快车速度为2a千米/小时，根据题意建立方程并求解，再设BC的表达式为y=kx+b，利用待定系数法即可求出BC的表达式，注意写出自变量x的取值范围；
（3）根据题意分别求出慢车行驶了5.5小时被第二辆快车追上，此时慢车行驶的路程以及第二辆快车行驶的路程也是440千米，第二辆快车追上慢车所需时间从而进行分析.
解：（1）根据图象可知甲、乙两地之间的距离为1200km，D的坐标为（15，1200）；
（2）设慢车速度为a千米/小时，
快车速度为2a千米/小时，根据题意得：
5（a+2a）=1200
解得：a=80， 2a=160，
因此慢车速度为80千米/小时，
快车速度为160千米/小时．
1200÷160=7.5
快车7.5小时到达乙地．
此时慢车与快车的距离为：7.5×80=600，C点坐标为（7.5，600）
设BC的表达式为y=kx+b，那么
，解得
，
∴BC的表达式为：y=240x-1200（5≤x≤7.5）；
（3）根据题意：慢车行驶了5.5小时被第二辆快车追上，此时慢车行驶的路程80×5.5=440，
第二辆快车行驶的路程也是440千米，第二辆快车追上慢车所需时间为：440÷160=2.75，
5．5-2.75=2.75
由于第一辆快车与慢车同时出发，所以第二辆快车比第一辆快车晚出发2.75小时．
