题目内容
【题目】已知,如图,矩形ABCD中,AD=2,AB=3,点E,F分别在边AB,BC上,且BF=FC,连接DE,EF,并以DE,EF为边作DEFG.
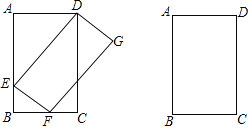
(1)求DEFG对角线DF的长;
(2)求DEFG周长的最小值;
(3)当DEFG为矩形时,连接BG,交EF,CD于点P,Q,求BP:QG的值.
【答案】(1)DF的长![]() ;(2)DEFG周长的最小值:
;(2)DEFG周长的最小值:![]() ;(3)BP:QG的值为
;(3)BP:QG的值为![]() 或
或![]() .
.
【解析】
(1)DEFG对角线DF的长就是Rt△DCF的斜边的长,由勾股定理求解;
(2)DEFG周长的最小值就是求邻边2(DE+EF)最小值,DE+EF的最小值就是以AB为对称轴,作点F的对称点M,连接DM交AB于点N,点E与N点重合时即DE+EF=DM时有最小值,在Rt△DMC中由勾股定理求DM的长;
(3)DEFG为矩形时有两种情况,一是一般矩形,二是正方形,分类用全等三角形判定与性质,等腰直角三角形判定与性质,三角形相似的判定与性质和勾股定理求解.
(1)如图1所示:
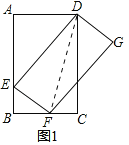
连接DF,
∵四边形ABCD是矩形,
∠C=90°,AD=BC,AB=DC,
∵BF=FC,AD=2;∴FC=1,
∵AB=3;∴DC=3,
在Rt△DCF中,由勾股定理得,
∴DF=![]() ;
;
故DEFG对角线DF的长![]() .
.
(2)如图2所示:
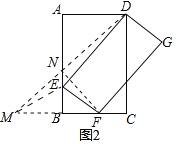
作点F关直线AB的对称点M,连接DM交AB于点N,
连接NF,ME,点E在AB上是一个动点,
①当点E不与点N重合时点M、E、D可构成一个三角形,
∴ME+DE>MD,
②当点E与点N重合时点M、E(N)、D在同一条直线上,
∴ME+DE=MD
由①和②DE+EF的值最小时就是点E与点N重合时,
∵MB=BF,∴MB=1,
∴MC=3,
又∵DC=3,
∴△MCD是等腰直角三角形,
∴MD=![]() ,
,
∴NF+DF=MD=2![]() ,
,
∴lDEFG=2(NF+DF)=4![]() ;
;
(3)①当AE=1,BE=2时,过点B作BH⊥EF,
如图3(甲)所示:
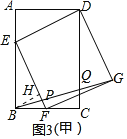
∵DEFG为矩形,
∴∠A=∠ABF=90°,
又∵BF=
∴在△ADE和△BEF中有,
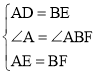 ,
,
∴△ADE≌△BEF中(SAS),
∴DE=EF,
∴矩形DEFG是正方形;
在Rt△EBF中,由勾股定理得:
EF=![]() ,
,
∴BH![]() ,
,
又∵△BEF~△FHB,
∴![]() ,
,
HF=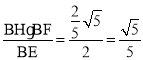 ,
,
在△BPH和△GPF中有:
![]() ,
,
∴△BPH∽△GPF(AA),
∴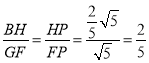
∴PF=![]() ,
,
又∵EP+PF=EF,
∴![]() ,
,
又∵AB∥BC,EF∥DG,
∴∠EBP=∠DQG,∠EPB=∠DGQ,
∴△EBP∽△DQG(AA),
∴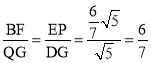 .
.
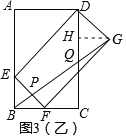
②当AE=2,BE=1时,过点G作GH⊥DC,
如图3(乙)所示:
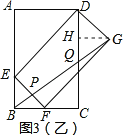
∵DEFG为矩形,
∴∠A=∠EBF=90°,
∵AD=AE=2,BE=BF=1,
∴在Rt△ADE和Rt△EFB中,由勾股定理得:
∴ED=![]() ,
,
EF=![]() ,
,
∴∠ADE=45°,
又∵四边形DEFG是矩形,
∴EF=DG,∠EDG=90°,
∴DG=![]() ,∠HDG=45°,
,∠HDG=45°,
∴△DHG是等腰直角三角形,
∴DH=HG=1,
在△HGQ和△BCQ中有,
![]()
∴△HGQ∽△BCQ(AA),
∴![]() ,
,
∵HC=HQ+CQ=2,
∴HQ=![]() ,
,
又∵DQ=DH+HQ,
∴DQ=1+![]() =
=![]() ,
,
∵AB∥DC,EF∥DG,
∴∠EBP=∠DQG,∠EPB=∠DGQ,
∴△EBP∽△DQG(AA),
∴![]() ,
,
综合所述,BP:QG的值为![]() 或
或![]() .
.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案【题目】为监控某条生产线上产品的质量,检测员每个相同时间抽取一件产品,并测量其尺寸,在一天的抽检结束后,检测员将测得的个数据按从小到大的顺序整理成如下表格:
编号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ | |||||
尺寸(cm) | 8.72 | 8.88 | 8.92 | 8.93 | 8.94 | 8.96 | 8.97 | 8.98 | a | 9.03 | 9.04 | 9.06 | 9.07 | 9.08 | b |
按照生产标准,产品等次规定如下:
尺寸(单位:cm) | 产品等次 |
8.97≤x≤9.03 | 特等品 |
8.95≤x≤9.05 | 优等品 |
8.90≤x≤9.10 | 合格品 |
x<8.90或x>9.10 | 非合格品 |
注:在统计优等品个数时,将特等品计算在内;在统计合格品个数时,将优等品(含特等品)仅算在内.
(1)已知此次抽检的合格率为80%,请判断编号为的产品是否为合格品,并说明理由
(2)已知此次抽检出的优等品尺寸的中位数为9cm.
(i)求a的值,
(ii)将这些优等品分成两组,一组尺寸大于9cm,另一组尺寸不大于9cm,从这两组中各随机抽取1件进行复检,求抽到的2件产品都是特等品的概率.