��Ŀ����
����Ŀ��������С����Ƶġ���ƽ���ı���һ���е㡱�ij߹���ͼ����.
��֪��ƽ���ı���ABCD.
��������M��ʹ��MΪ��AD���е�.

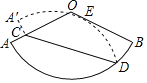
��������ͼ��
��������BA��
���Ե�AΪԲ�ģ�CD��Ϊ�뾶��������BA���ӳ����ڵ�E��
������EC��AD�ڵ�M��
���Ե�M�����������ĵ㣮
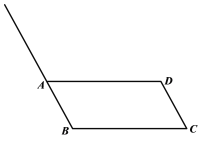
����С����Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ�������ͼ�ۼ�����
��2����������֤����
֤��������AC��ED��
���ı���ABCD��ƽ���ı��Σ�
��![]() ��
��
��AE= ��
���ı���EACD��ƽ���ı��Σ� ���������������ݣ���
��![]() �� ���������������ݣ���
�� ���������������ݣ���
����MΪ�������ı�AD���е㣮
���𰸡���1�������������2����![]() ��һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ�ƽ���ı��εĶԽ�����ƽ��.
��һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ�ƽ���ı��εĶԽ�����ƽ��.
��������
��1������������ͼ����
��2������ƽ���ı��ε��ж������ʼ��ɵó���.
�⣺��1����ȫ��ͼ����ͼ��ʾ��
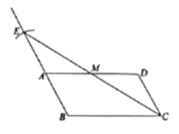
��2����Ϊ![]() ����Ҫʹ���ı���EACD��ƽ���ı��Σ���ȱ��
����Ҫʹ���ı���EACD��ƽ���ı��Σ���ȱ��![]() ���ʴ�Ϊ
���ʴ�Ϊ![]() ����������Ϊһ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ�����ƽ���ı��ε����ʿ�֪ƽ���ı��εĶԽ�����ƽ��.
����������Ϊһ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ�����ƽ���ı��ε����ʿ�֪ƽ���ı��εĶԽ�����ƽ��.

��ϰ��ϵ�д�
�����Ŀ