题目内容
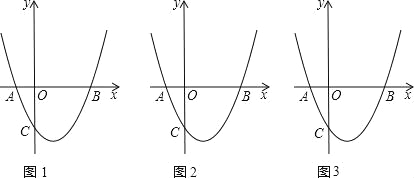
【题目】如图1,抛物线y=x2﹣2x+k与x轴交于点A、B两点,与y轴交于点C(0,﹣3)(图2,图3为解答备用图).
(1)k= ,点A的坐标为 ,点B的坐标为 ;
(2)设抛物线y=x2﹣2x+k的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.
【答案】(1)﹣3,(﹣1,0),(3,0);
(2)S四边形ABMC=9;
(3)当m=![]() 时,S四边形ABDC最大,此时D(
时,S四边形ABDC最大,此时D(![]() ,﹣
,﹣![]() ).
).
【解析】
试题分析:(1)将C点坐标代入抛物线解析式可求k的值,由抛物线解析式求A,B两点坐标;
(2)根据A、B、M、N四点坐标,将四边形分割为两个三角形和一个梯形求面积;
(3)只要使△DBC面积最大即可,由此求D点坐标;
试题解析:(1)将C(0,﹣3)代入抛物线y=x2﹣2x+k中,得k=﹣3,
∴抛物线解析式为y=x2﹣2x﹣3,
令y=0,得x=﹣1或3,
∴A(﹣1,0),B(3,0);
故答案为﹣3,(﹣1,0),(3,0);
(2)如图(1),
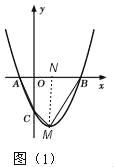
过M点作MN⊥AB,垂足为N,
由y=x2﹣2x﹣3=(x﹣1)2﹣4,可知M(1,﹣4),
∴S四边形ABMC=S△ACO+S梯形OCMN+S△BMN=![]() ×1×3+
×1×3+![]() ×(3+4)×1+
×(3+4)×1+![]() ×(3﹣1)×4=9;
×(3﹣1)×4=9;
(3)存在,如图(2),
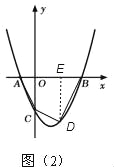
设D(m,m2﹣2m﹣3),
过D点作DE⊥AB,垂足为E,则
S四边形ABDC=S△ACO+S梯形OCDE+S△BDE
=![]() ×1×3+
×1×3+![]() ×[3﹣(m2﹣2m﹣3)]×m+
×[3﹣(m2﹣2m﹣3)]×m+![]() ×(3﹣m)×[﹣(m2﹣2m﹣3)]
×(3﹣m)×[﹣(m2﹣2m﹣3)]
=﹣![]() m2+
m2+![]() m+6,
m+6,
∵﹣![]() <0,
<0,
∴当m=﹣![]() =
=![]() 时,S四边形ABDC最大,此时D(
时,S四边形ABDC最大,此时D(![]() ,﹣
,﹣![]() ).
).

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目

