��Ŀ����
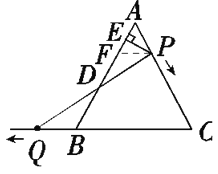
����Ŀ����ͼ����ABC�DZ߳�Ϊ6�ĵȱ������Σ�P��AC����һ���㣬��A��C�˶�����A��C���غϣ���Q��CB�ӳ�����һ���㣬���Pͬʱ����ͬ���ٶ���B��CB�ӳ��߷����˶���Q����B�غϣ�����P��PE��AB��E������PQ��AB��D��
��1����AE=1ʱ����AP�ij���
��2������BQD=30��ʱ����AP�ij���
��3�����˶��������߶�ED�ij��Ƿ����仯��������䣬����߶�ED�ij�����������仯����˵������.

���𰸡���1��2����2��2����3��DE=3������.
�������������������1���ɡ�APF�ǵȱ���������PE��AF���õ���APE=30�㣬��30������ֱ�DZߵ���б�ߵ�һ�룬�õ����ۣ�
��2����P��PF��QC������AFP�ǵȱ������Σ��ɵõ���DBQ�ա�DFP���õ���BQD=��BDQ=��FDP=��FPD=30�㣬�õ�BD=DF=FA���Ӷ��õ����ۣ�
��3���ɣ�2���õ�BD=DF���õ�DE+DF+EF=AB=6���Ӷ��õ�DE=3��Ϊ��ֵ��
����������⣺��1���ߡ�APF�ǵȱ������������A=60������PE��AF�����APE=30����
��AE=1����APE=30����PE��AF����AP=2AE=2��
��2����![]() ��PF��QC������AFP�ǵȱ������Σ�
��PF��QC������AFP�ǵȱ������Σ�
��![]() ͬʱ�������ٶ���ͬ����
ͬʱ�������ٶ���ͬ����![]() ��
��
��![]() ����
����![]() ����
����![]() ��
��
��![]()
��![]()
![]()
��3���ɣ�2��֪![]() ����
����![]() �ǵȱ������Σ�
�ǵȱ������Σ� ![]() ��
��
��![]()
![]() ��
��![]()
��![]() Ϊ��ֵ����
Ϊ��ֵ����![]() �ij�������
�ij�������

 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�

