题目内容
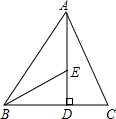 如图在△ABC中,AD是BC边上的高,BE平分∠ABD,交AD于E.已知∠BED=60°,∠BAC=50°,则∠C=
如图在△ABC中,AD是BC边上的高,BE平分∠ABD,交AD于E.已知∠BED=60°,∠BAC=50°,则∠C=
- A.70°
- B.50°
- C.60°
- D.30°
A
分析:由AD是BC边上的高得∠ADB=90°,根据三角形的内角和定理得到∠DBE=90°-∠BED=90°-60°=30°,根据角平分线的定义由BE平分∠ABD得∠ABD=2∠DBE=2×30°=60°,然后再根据角形的内角和定理有∠BAC+∠ABC+∠C=180°,把∠BAC=50°,∠ABD=60°代入计算即可得到∠C的度数.
解答:∵AD是BC边上的高,
∴∠ADB=90°,
∵∠BED=60°,
∴∠DBE=90°-60°=30°,
又∵BE平分∠ABD,
∴∠ABD=2∠DBE=2×30°=60°,
而∠BAC+∠ABC+∠C=180°,∠BAC=50°,
∴∠C=180°-60°-50°=70°.
故选A.
点评:本题考查了三角形的内角和定理:三角形的内角和为180°.也考查了角平分线的定义.
分析:由AD是BC边上的高得∠ADB=90°,根据三角形的内角和定理得到∠DBE=90°-∠BED=90°-60°=30°,根据角平分线的定义由BE平分∠ABD得∠ABD=2∠DBE=2×30°=60°,然后再根据角形的内角和定理有∠BAC+∠ABC+∠C=180°,把∠BAC=50°,∠ABD=60°代入计算即可得到∠C的度数.
解答:∵AD是BC边上的高,
∴∠ADB=90°,
∵∠BED=60°,
∴∠DBE=90°-60°=30°,
又∵BE平分∠ABD,
∴∠ABD=2∠DBE=2×30°=60°,
而∠BAC+∠ABC+∠C=180°,∠BAC=50°,
∴∠C=180°-60°-50°=70°.
故选A.
点评:本题考查了三角形的内角和定理:三角形的内角和为180°.也考查了角平分线的定义.

练习册系列答案
相关题目
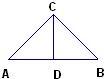
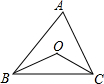 如图在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,则∠BOC的度数为
如图在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,则∠BOC的度数为 如图在△ABC中,∠A=45°,tanB=3,BC=
如图在△ABC中,∠A=45°,tanB=3,BC= 已知,如图在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG平分∠CDE,DC=AE,
已知,如图在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG平分∠CDE,DC=AE,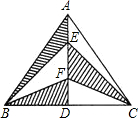 如图在△ABC中,AD垂直平分BC,AD=8,BC=10,E、F是AD上的两点,则图中阴影部分的面积是
如图在△ABC中,AD垂直平分BC,AD=8,BC=10,E、F是AD上的两点,则图中阴影部分的面积是