题目内容
【题目】四条直线两两相交，且任意三条不相交于同一点，则四条直线共可构成的同位角有组
【答案】48
【解析】解：如图，以直线a,b,c相交时，能构成4+4+4=12组同位角；
以直线a,b,d相交时，能构成4+4+4=12组同位角；
以直线a,c,d相交时，能构成4+4+4=12组同位角；
以直线b,c,d相交时，能构成4+4+4=12组同位角；
所以一共可以构成12+12+12+12=48组同位角.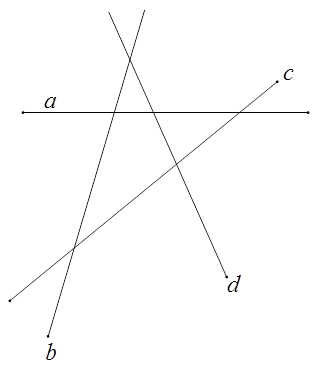
所以答案是48.
【考点精析】本题主要考查了同位角、内错角、同旁内角的相关知识点，需要掌握两条直线被第三条直线所截形成八个角，它们构成了同位角、内错角与同旁内角;判别同位角、内错角或同旁内角的关键是找到构成这两个角的“三线”，有时需要将有关的部分“抽出”或把无关的线略去不看，有时又需要把图形补全才能正确解答此题．
练习册系列答案
相关题目
