��Ŀ����
����Ŀ����ͼ�����㹻��ı߳�Ϊa��С�����Σ�A�ࣩ����Ϊa��Ϊb�ij����Σ�B�ࣩ�Լ��߳�Ϊb�Ĵ������Σ�C�ࣩ����������ͼ���е����ֲ������ɿ���ƴ��һЩ������������ijЩ��ʽ��
���Խ����
��1��ȡͼ���е����ɸ�������ͼ�ζ�Ҫȡ����ƴ��һ�������Σ�ʹ�����Ϊ��a+b����a+b�������������߿��л���ͼ�Σ�������ͼ�λش�a+b����a+b��= ��
��2��ͼ������ͼ���е����ֲ���ƴ����һ�������Σ����ݢڿ��Եõ������͵�ʽ��
��3����ȡ���е����ɸ�������ͼ�ζ�Ҫȡ����ƴ��һ�������Σ�ʹ�����Ϊ3a2+4ab+b2 �� �㻭��ͼ����ҪB�Ƭ�ţ�
��4���ֽ���ʽ��3a2+4ab+b2 ��
��չ�о�����ͼ�ۣ��������εı߳�Ϊm��С�����εı߳�Ϊn������m��n��ʾ�ĸ�ֱ�������ε���ֱ�DZ߱߳���b��a�����۲�ͼ�������¹�ϵʽ����ȷ���� �� ����д��ȷѡ�����ţ�
��1��ab= ![]()
��2��a+b=m
��3��a2+b2= ![]()
��4��a2+b2=m2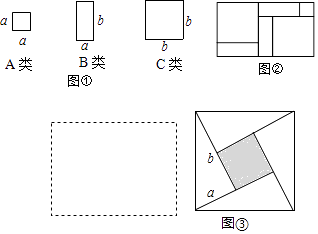
���𰸡�
��1��a2+2ab+b2
��2��a2+3ab+2b2
��3��4
��4����1������4��
���������⣺��1����ͼ��
��a+b����a+b��=a2+2ab+b2 ��
���Դ��ǣ�a2+2ab+b2����2�������ε����Ϊa2+3ab+2b2 ��
���Դ��ǣ�a2+3ab+2b2 �� ��3����3a2+4ab+b2=��3a+b����a+b����
����ҪB�Ƭ4�ţ�
���Դ��ǣ�4����4���⣺����ͼ�۵ã�4�� ![]() ab+n2=m2 ��
ab+n2=m2 ��
��ab= ![]() ��
��
�ߣ�b��a��2=n2 �� 4�� ![]() ab+n2=2ab+��b��a��2=m2 ��
ab+n2=2ab+��b��a��2=m2 ��
��a2+b2=m2 ��
�ࣨ1������4����ȷ��
���Դ��ǣ���1������4����