题目内容
【题目】如图,将矩形ABCD沿对角线BD所在直线折叠,点C落在同一平面内,落点记为C′,BC′与AD交于点E,若AB=3,BC=4,则DE的长为 . 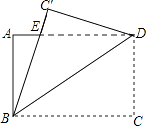
【答案】![]()
【解析】解:由折叠得,∠CBD=∠EBD,
由AD∥BC得,∠CBD=∠EDB,
∴∠EBD=∠EDB,
∴DE=BE,
设DE=BE=x,则AE=4﹣x,
在直角三角形ABE中,AE2+AB2=BE2 , 即(4﹣x)2+32=x2 ,
解得x= ![]() ,
,
∴DE的长为 ![]() .
.
所以答案是: ![]()
【考点精析】关于本题考查的勾股定理的概念和矩形的性质,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等才能得出正确答案.

练习册系列答案
相关题目