题目内容
如图(1),矩形ABCD的一边BC在直角坐标系中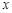 轴上,折叠边AD,使点D落在
轴上,折叠边AD,使点D落在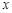 轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为
轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为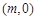 ,其中
,其中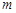 >0.
>0.
(1)求点E、F的坐标(用含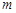 的式子表示);
的式子表示);
(2)连接OA,若△OAF是等腰三角形,求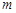 的值;
的值;
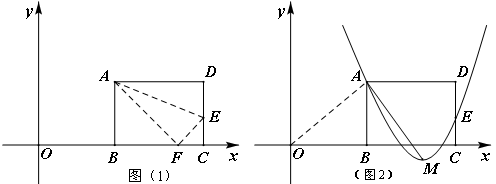
(3)设抛物线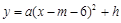 经过图(1)中的A、E两点,如图(2),其顶点为M,连结AM,若∠OAM=90°,求
经过图(1)中的A、E两点,如图(2),其顶点为M,连结AM,若∠OAM=90°,求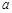 、
、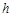 、
、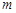 的值.
的值.
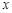 轴上,折叠边AD,使点D落在
轴上,折叠边AD,使点D落在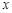 轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为
轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为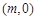 ,其中
,其中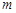 >0.
>0.
(1)求点E、F的坐标(用含
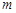 的式子表示);
的式子表示); (2)连接OA,若△OAF是等腰三角形,求
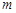 的值;
的值; (3)设抛物线
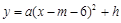 经过图(1)中的A、E两点,如图(2),其顶点为M,连结AM,若∠OAM=90°,求
经过图(1)中的A、E两点,如图(2),其顶点为M,连结AM,若∠OAM=90°,求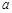 、
、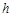 、
、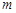 的值.
的值. (1)E(m+10,3),F(m+6,0);(2)6或4或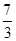 ;(3)
;(3)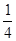 ,-1,12
,-1,12
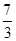 ;(3)
;(3)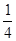 ,-1,12
,-1,12试题分析:(1)∵根据矩形的性质可得AD=BC=10,AB=CD=8,∠D=∠DCB=∠ABC=90°,由折叠对称性可得AF=AD=10,FE=DE,在Rt△ABF中,根据勾股定理可求得BF的长,从而可得FC的长,设DE=x,在Rt△ECF中,根据勾股定理即可列方程求得x的值,从而得到CE的长,即得结果;
(2)分三种情形讨论:若AO=AF,若OF=AF,若AO=OF,根据等腰三角形的性质及勾股定理求解;
(3)由(1)知A(m,8),E(m+10,3),再代入抛物线
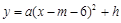 即可求得
即可求得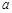 、
、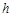 的值,从而表示出点M的坐标,设对称轴交AD于G,即可表示出点G的坐标,求得AG、GM的长,再证得△AOB∽△AMG,根据相似三角形的性质即可求得结果.
的值,从而表示出点M的坐标,设对称轴交AD于G,即可表示出点G的坐标,求得AG、GM的长,再证得△AOB∽△AMG,根据相似三角形的性质即可求得结果.(1)∵四边形ABCD是矩形,
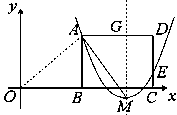
∴AD=BC=10,AB=CD=8,∠D=∠DCB=∠ABC=90°.
由折叠对称性:AF=AD=10,FE=DE.
在Rt△ABF中,BF=
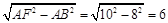 .
.∴FC="4."
设DE=x,在Rt△ECF中,
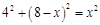 ,解得
,解得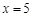
∴CE=
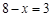
∵B(m,0)
∴E(m+10,3),F(m+6,0);
(2)分三种情形讨论:
若AO=AF,∵AB⊥OF,∴OB=BF=6.∴m=6.
若OF=AF,则m+6=10,解得m=4.
若AO=OF,在Rt△AOB中,AO2=OB2+AB2=m2+64,
∴
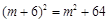 ,解得m=
,解得m=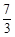 .
. 综合得m=6或4或
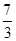 ;
;(3)由(1)知A(m,8),E(m+10,3).
由题意得
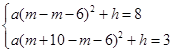 , 解得
, 解得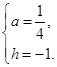
∴M(m+6,﹣1).
设对称轴交AD于G.
∴G(m+6,8),
∴AG=6,GM=
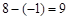
∵∠OAB+∠BAM=90°,∠BAM+∠MAG=90°,
∴∠OAB=∠MAG.
又∵∠ABO=∠MGA=90°,
∴△AOB∽△AMG.
∴
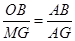 ,即
,即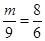
∴m=12.
点评:二次函数的综合题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.

练习册系列答案
相关题目
 与y轴正半轴交于点C,连接BC、AC,CD是⊙
与y轴正半轴交于点C,连接BC、AC,CD是⊙ ,抛物线
,抛物线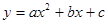 过A、B、C三点.
过A、B、C三点.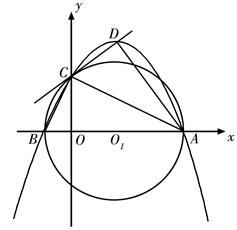
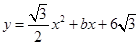 经过A(2,0). 设顶点为点P,与x轴的另一交点为点B.
经过A(2,0). 设顶点为点P,与x轴的另一交点为点B.
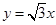 上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐标;若不存在,请说明理由;
上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐标;若不存在,请说明理由;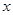 轴下方的抛物线上是否存在点M,使△AMP≌△AMB?如果存在,试举例验证你的猜想;如果不存在,试说明理由.
轴下方的抛物线上是否存在点M,使△AMP≌△AMB?如果存在,试举例验证你的猜想;如果不存在,试说明理由.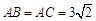 ,经过这个三角形重心的直线DE // BC,分别交边AB、AC于点D和点E,P是线段DE上的一个动点,过点P分别作PM⊥BC,PF⊥AB,PG⊥AC,垂足分别为点M、F、G.设BM = x,四边形AFPG的面积为y.
,经过这个三角形重心的直线DE // BC,分别交边AB、AC于点D和点E,P是线段DE上的一个动点,过点P分别作PM⊥BC,PF⊥AB,PG⊥AC,垂足分别为点M、F、G.设BM = x,四边形AFPG的面积为y.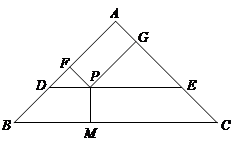
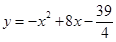 与
与 轴所围成的封闭图形染成红色,则在此红色内部区域及其边界上的
轴所围成的封闭图形染成红色,则在此红色内部区域及其边界上的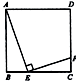
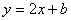 交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.