题目内容
如图,在平面直角坐标系xOy中,AB在x轴上,AB=10,以AB为直径的⊙ 与y轴正半轴交于点C,连接BC、AC,CD是⊙
与y轴正半轴交于点C,连接BC、AC,CD是⊙ 的切线,AD⊥CD于点D,tan∠CAD=
的切线,AD⊥CD于点D,tan∠CAD=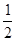 ,抛物线
,抛物线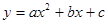 过A、B、C三点.
过A、B、C三点.
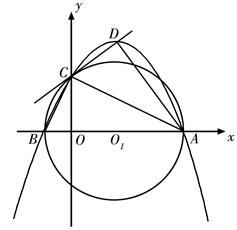
(1)求证:∠CAD=∠CAB;
(2)求抛物线的解析式;
(3)判断抛物线的顶点E是否在直线CD上,并说明理由.
 与y轴正半轴交于点C,连接BC、AC,CD是⊙
与y轴正半轴交于点C,连接BC、AC,CD是⊙ 的切线,AD⊥CD于点D,tan∠CAD=
的切线,AD⊥CD于点D,tan∠CAD=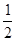 ,抛物线
,抛物线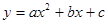 过A、B、C三点.
过A、B、C三点.
(1)求证:∠CAD=∠CAB;
(2)求抛物线的解析式;
(3)判断抛物线的顶点E是否在直线CD上,并说明理由.
(1)证明∠ CA=∠CAD,∠CAB=∠
CA=∠CAD,∠CAB=∠ CA,得∠CAD=∠CAB;(2)
CA,得∠CAD=∠CAB;(2)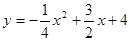 (3)抛物线顶点E在直线CD上;理由将E(3,
(3)抛物线顶点E在直线CD上;理由将E(3,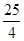 )代入直线DC的解析式y=
)代入直线DC的解析式y=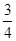 x+4中,右边=
x+4中,右边=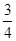 ×3+4=
×3+4=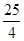 =左边,得抛物线顶点E在直线CD上
=左边,得抛物线顶点E在直线CD上
 CA=∠CAD,∠CAB=∠
CA=∠CAD,∠CAB=∠ CA,得∠CAD=∠CAB;(2)
CA,得∠CAD=∠CAB;(2)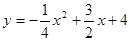 (3)抛物线顶点E在直线CD上;理由将E(3,
(3)抛物线顶点E在直线CD上;理由将E(3,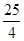 )代入直线DC的解析式y=
)代入直线DC的解析式y=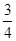 x+4中,右边=
x+4中,右边=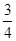 ×3+4=
×3+4=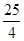 =左边,得抛物线顶点E在直线CD上
=左边,得抛物线顶点E在直线CD上试题分析:(1)证明:连接
 C,
C,∵CD是⊙
 的切线,
的切线,∴
 C⊥CD,
C⊥CD,∵AD⊥CD,
∴
 C∥AD,
C∥AD,∴∠
 CA=∠CAD,
CA=∠CAD,∵
 A=
A= C,
C,∴∠CAB=∠
 CA,
CA,∴∠CAD=∠CAB;
(2)解:①∵AB是⊙
 的直径,
的直径,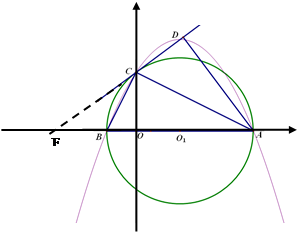
∴∠ACB=90°,
∵OC⊥AB,
∴∠CAB=∠OCB,
∴△CAO∽△BCO,
∴
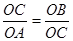 ,
,即OC2=OA•OB,
∵tan∠CAO=tan∠CAD=
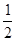 ,
,∴AO=2CO,
又∵AB=10,
∴OC2=2CO(10-2CO),
∵CO>0,
∴CO=4,AO=8,BO=2,
∴A(8,0),B(-2,0),C(0,4),
∵抛物线y=ax2+bx+c过点A,B,C三点,
∴c=4,
由题意得:
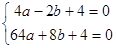 ,
,解得:
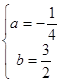 ,
,∴抛物线的解析式为:
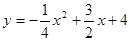 ;
; ②设直线DC交x轴于点F,
∴△AOC≌△ADC,
∴AD=AO=8,
∵
 C∥AD,
C∥AD,∴△F
 C∽△FAD,
C∽△FAD,∴
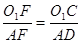 ,
,∴8(BF+5)=5(BF+10),
∴BF=
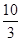 ,F(
,F(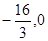 );
); 设直线DC的解析式为y=kx+m,则
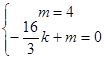 ,
,解得:
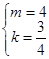 ?,
?,∴直线DC的解析式为y=
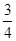 x+4,
x+4,由
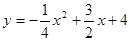 =
=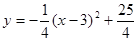 得顶点E的坐标为(3,
得顶点E的坐标为(3,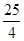 ),
),将E(3,
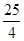 )代入直线DC的解析式y=
)代入直线DC的解析式y=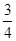 x+4中,
x+4中,右边=
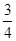 ×3+4=
×3+4=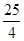 =左边,
=左边,∴抛物线顶点E在直线CD上;
点评:本题考查抛物线,要求考生会用待定系数法求抛物线的解析式,会判断一个点是否在函数图象上

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的图象与
的图象与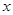 轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
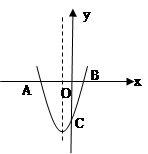
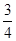 x与BC边相交于D点.
x与BC边相交于D点.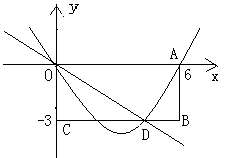
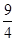 x经过点A,试确定此抛物线的解析式;
x经过点A,试确定此抛物线的解析式;
 (米)与水平距离
(米)与水平距离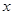 (米)满足关系式为:
(米)满足关系式为: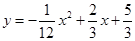 ,则小林这次铅球推出的距离是 米.
,则小林这次铅球推出的距离是 米. 轴上,折叠边AD,使点D落在
轴上,折叠边AD,使点D落在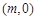 ,其中
,其中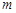 >0.
>0.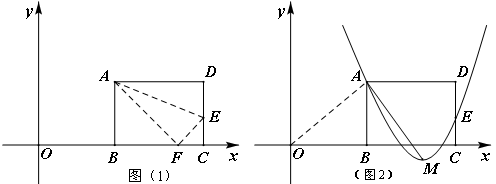
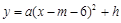 经过图(1)中的A、E两点,如图(2),其顶点为M,连结AM,若∠OAM=90°,求
经过图(1)中的A、E两点,如图(2),其顶点为M,连结AM,若∠OAM=90°,求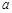 、
、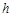 、
、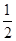 x2-
x2-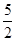 x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t .
x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t .