题目内容
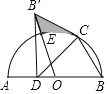
【题目】已知梯形![]() 中,
中,![]() ∥
∥![]() ,且
,且![]() ,
,![]() ,
,![]() 。
。
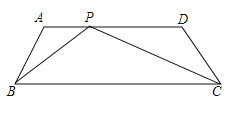
⑴如图,P为![]() 上的一点,满足∠BPC=∠A,求AP的长;
上的一点,满足∠BPC=∠A,求AP的长;
⑵如果点P在![]() 边上移动(点P与点
边上移动(点P与点![]() 不重合),且满足∠BPE=∠A,
不重合),且满足∠BPE=∠A,![]() 交直线
交直线![]() 于点E,同时交直线DC于点
于点E,同时交直线DC于点![]() 。
。
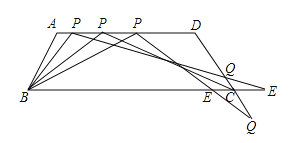
①当点![]() 在线段DC的延长线上时,设
在线段DC的延长线上时,设![]() ,CQ=y,求
,CQ=y,求![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
②写CE=1时,写出AP的长(不必写解答过程)
【答案】⑴![]() 的长1或4;⑵①
的长1或4;⑵①![]()
![]() ;②
;②![]() 或3-
或3-![]()
【解析】
(1)当∠BPC=∠A时,∠A+∠APB+∠ABP=180°,而∠APB+∠BPC+∠DPC=180°,因此∠ABP=∠DPC,此时三角形APB与三角形DPC相似,那么可得出关于AP,PD,AB,CD的比例关系式,AB,CD的值题中已经告诉,可以先用AP表示出PD,然后代入上面得出的比例关系式中求出AP的长.
(2)①与(1)的方法类似,只不过把DC换成了DQ,那么只要用DC+CQ就能表示出DQ了.然后按得出的关于AB,AP,PD,DQ的比例关系式,得出x,y的函数关系式.
②和①的方法类似,但是要多一步,要先通过平行得出三角形PDQ和CEQ相似,根据CE的长,用AP表示出PD,然后根据PD,DQ,QC,CE的比例关系用AP表示出DQ,然后按①的步骤进行求解即可.
解:⑴![]() ,
,![]() ,
,
![]() ,
,
又![]() 梯形
梯形![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,
,![]() ,
,
![]() ,
,
解得![]() ,
,![]() ,
,
![]() 的长1或4;
的长1或4;
⑵①由⑴易得![]() (如图),
(如图),
![]() ,即
,即![]() ,
,
![]()
![]()
②当CE=1时,
∵△PDQ∽△ECQ,
∴![]() ,
,
![]() 或
或![]() ,
,
![]() ,
,
解得:AP=2或3![]() .
.

练习册系列答案
相关题目