题目内容
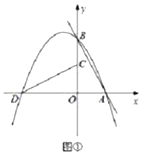
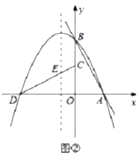
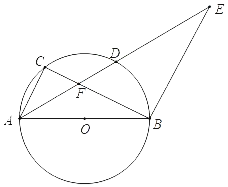
【题目】如图,AB是⊙O的直径,点C是圆上一点,点D是![]() 的中点,延长AD至点E,使得AB=BE.
的中点,延长AD至点E,使得AB=BE.
(1)求证:△ACF∽△EBF;
(2)若BE=10,tanE=![]() ,求CF的长.
,求CF的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)由圆周角定理及等腰三角形的性质可得出∠CAF=∠E,结合对顶角相等(∠AFC=∠EFB)可证出△ACF∽△EBF;
(2)由AB为直径可得出∠ACB=90°,利用相似三角形的性质可得出∠EBF=90°,由BE=10,tanE=![]() 结合相似三角形的性质可得出BF=
结合相似三角形的性质可得出BF=![]() ,AC=3CF,在Rt△ABC中利用勾股定理可得出关于CF长度的一元二次方程,解之取其正值即可得出结论.
,AC=3CF,在Rt△ABC中利用勾股定理可得出关于CF长度的一元二次方程,解之取其正值即可得出结论.
(1)证明:∵点D是![]() 的中点,
的中点,
∴∠CAD=∠BAE.
∵AB=BE,
∴∠BAE=∠E,
∴∠CAF=∠E.
又∵∠AFC=∠EFB,
∴△ACF∽△EBF;
(2)解:∵AB为⊙O的直径,
∴∠ACB=90°.
∵△ACF∽△EBF,
∴∠EBF=∠ACF=90°.
∵BE=10,tanE=![]() ,
,
∴BF=BEtanE=![]() .
.
∵∠CAF=∠E,
∴AC=3CF.
在Rt△ABC中,∠ACB=90°,AB=BE=10,AC=3CF,BC=CF+![]() ,
,
∴AB2=AC2+BC2,即102=9CF2+(CF+![]() )2,
)2,
解得:CF=![]() 或CF=﹣
或CF=﹣![]() (舍去).
(舍去).
∴CF的长为![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成m种不同的等腰三角形,为探究m与n之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
(1)用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?此时,显然能搭成一种等腰三角形.所以,当n=3时,m=1
(2)用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形,所以,当n=4时,m=0
(3)用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形?若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形,所以,当n=5时,m=1
(4)用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形?若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形,所以,当n=6时,m=1
综上所述,可得表①
n | 3 | 4 | 5 | 6 |
m | 1 | 0 | 1 | 1 |
探究二:
(1)用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?(仿照上述探究方法,写出解答过程,并把结果填在表②中)
(2)分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?(只需把结果填在表②中)
n | 7 | 8 | 9 | 10 |
m |
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,…
解决问题:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设n分别等于4k﹣1、4k、4k+1、4k+2,其中k是整数,把结果填在表 ③中)
n | 4k﹣1 | 4k | 4k+1 | 4k+2 |
m |
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(要求写出解答过程)其中面积最大的等腰三角形每个腰用了 根木棒.(只填结果)