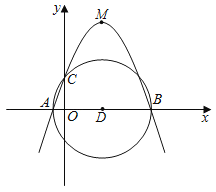题目内容
【题目】在平面直角坐标系中,二次函数 y=ax2+bx+2 的图象与 x 轴交于 A(﹣3,0),B(1,0)两点,与 y 轴交于点C.
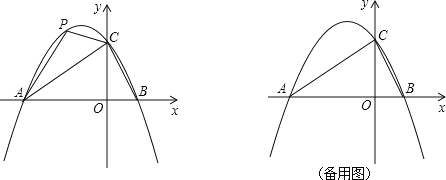
(1)求这个二次函数的关系解析式 ,x 满足什么值时 y﹤0 ?
(2)点 p 是直线 AC 上方的抛物线上一动点,是否存在点 P,使△ACP 面积最大?若存在,求出点 P的坐标;若不存在,说明理由
(3)点 M 为抛物线上一动点,在 x 轴上是否存在点 Q,使以 A、C、M、Q 为顶点的四边形是平行四边形?若存在,直接写出点 Q 的坐标;若不存在,说明理由.
【答案】(1)![]() ,
,![]() 或
或![]() ;(2)P
;(2)P![]() ;(3)
;(3)![]()
【解析】
(1)将点A(﹣3,0),B(1,0)带入y=ax2+bx+2得到二元一次方程组,解得即可得出函数解析式;又从图像可以看出x 满足什么值时 y﹤0;
(2)设出P点坐标![]() ,利用割补法将△ACP 面积转化为
,利用割补法将△ACP 面积转化为![]() ,带入各个三角形面积算法可得出
,带入各个三角形面积算法可得出![]() 与m之间的函数关系,分析即可得出面积的最大值;
与m之间的函数关系,分析即可得出面积的最大值;
(3)分两种情况讨论,一种是CM平行于x轴,另一种是CM不平行于x轴,画出点Q大概位置,利用平行四边形性质即可得出关于点Q坐标的方程,解出即可得到Q点坐标.
解:(1)将A(﹣3,0),B(1,0)两点带入y=ax2+bx+2可得:
![]()
解得: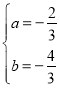
∴二次函数解析式为![]() .
.
由图像可知,当![]() 或
或![]() 时y﹤0;
时y﹤0;
综上:二次函数解析式为![]() ,当
,当![]() 或
或![]() 时y﹤0;
时y﹤0;
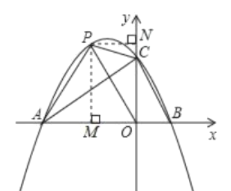
(2)设点P坐标为![]() ,如图连接PO,作PM⊥x轴于M,PN⊥y轴于N.
,如图连接PO,作PM⊥x轴于M,PN⊥y轴于N.
PM=![]() ,PN=
,PN=![]() ,AO=3.
,AO=3.
当![]() 时,
时,![]() ,所以OC=2
,所以OC=2
![]()
![]() ,
,
∵![]()
∴函数![]() 有最大值,
有最大值,
当![]() 时,
时,![]() 有最大值,
有最大值,
此时![]() ;
;
所以存在点![]() ,使△ACP 面积最大.
,使△ACP 面积最大.
(3)存在,![]()
假设存在点Q使以 A、C、M、Q 为顶点的四边形是平行四边形
①若CM平行于x轴,如下图,有符合要求的两个点![]() 此时
此时![]() =
=![]()
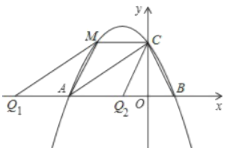
∵CM∥x轴,
∴点M、点C(0,2)关于对称轴![]() 对称,
对称,
∴M(﹣2,2),
∴CM=2.
由![]() =
=![]()
![]() ;
;
②若CM不平行于x轴,如下图,过点M作MG⊥x轴于点G,
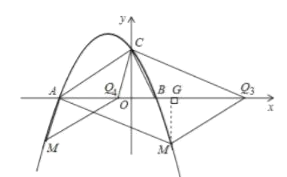
易证△MGQ≌△COA,得QG=OA=3,MG=OC=2,即![]() .
.
设M(x,﹣2),则有![]() ,解得:
,解得:![]() .
.
又QG=3,∴![]() ,
,
∴![]()
综上所述,存在点P使以 A、C、M、Q 为顶点的四边形是平行四边形,
Q点坐标为:
![]() .
.

【题目】某校九年级学生某科目学期总评成绩是由完成作业、单元检测、期末考试三项成绩构成的,如果学期总评成绩80分以上(含80分),则评定为“优秀”,下表是小张和小王两位同学的成绩记录:
完成作业 | 单元测试 | 期末考试 | |
小张 | 70 | 90 | 80 |
小王 | 60 | 75 | _______ |
若按完成作业、单元检测、期末考试三项成绩按1:2:7的权重来确定学期总评成绩.
(1)请计算小张的学期总评成绩为多少分?
(2)小王在期末(期末成绩为整数)应该最少考多少分才能达到优秀?
【题目】每年夏季全国各地总有未成年人因溺水而丧失生命,令人痛心疾首.今年某校为确保学生安全,开展了“远离溺水珍爱生命”的防溺水安全知识竞赛.现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示,共分成四组:A.80≤x<85,B.85≤x<90,C.90≤x<95,D.95≤x≤100),下面给出了部分信息:七年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82;八年级10名学生的竞赛成绩在C组中的数据是:94,90,94.
七、八年级抽取的学生竞赛成绩统计表
年级 | 七年级 | 八年级 |
平均数 | 92 | 92 |
中位数 | 93 | b |
众数 | c | 100 |
方差 | 52 | 50.4 |
根据以上信息,解答下列问题:
(1)直接写出上述图表中a,b,c的值;
(2)根据以上数据,你认为该校七、八年级中哪个年级学生掌握防溺水安全知识较好?请说明理由(一条理由即可);
(3)该校七、八年级共720人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀(x≥90)的学生人数是多少?