题目内容
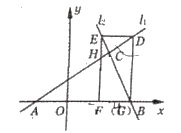
【题目】如图,一个斜边长为10cm的红色三角形纸片,一个斜边长为6cm的蓝色三角形纸片,一张黄色的正方形纸片,拼成一个直角三角形,则红、蓝两张纸片的面积之和是( )
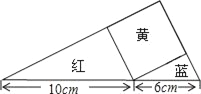
A. 60cm2 B. 50cm2 C. 40cm2 D. 30cm2
【答案】D
【解析】分析:标注字母,根据两直线平行,同位角相等可得∠B=∠AED,然后求出△ADE和△EFB相似,根据相似三角形对应边成比例求出![]() ,即
,即![]() ,设BF=3a,表示出EF=5a,再表示出BC、AC,利用勾股定理列出方程求出a的值,再根据红、蓝两张纸片的面积之和等于大三角形的面积减去正方形的面积计算即可得解.
,设BF=3a,表示出EF=5a,再表示出BC、AC,利用勾股定理列出方程求出a的值,再根据红、蓝两张纸片的面积之和等于大三角形的面积减去正方形的面积计算即可得解.
如图,∵正方形的边DE∥CF,
∴∠B=∠AED,
∵∠ADE=∠EFB=90°,
∴△ADE∽△EFB,
∴![]() ,
,
∴![]() ,
,
设BF=3a,则EF=5a,
∴BC=3a+5a=8a,
AC=8a×![]() =
=![]() a,
a,
在Rt△ABC中,AC2+BC2=AB2,
即(![]() a)2+(8a)2=(10+6)2,
a)2+(8a)2=(10+6)2,
解得a2=![]() ,
,
红、蓝两张纸片的面积之和=![]() ×
×![]() a×8a-(5a)2,
a×8a-(5a)2,
=![]() a2-25a2,
a2-25a2,
=![]() a2,
a2,
=![]() ×
×![]() ,
,
=30cm2.
故选D.

练习册系列答案
相关题目