Question

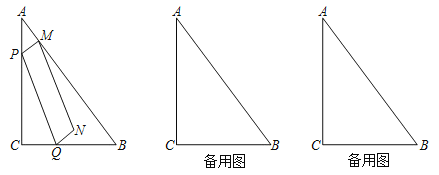
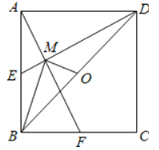
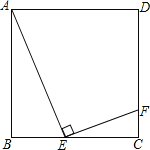
【题目】如图，已知边长为1的正方形ABCD，在BC边上有一动点E，连接AE，作EF⊥AE，交CD边于点F．设BE＝x，CF＝y．

（1）写出y与x的函数关系式．

（2）CF的长可能等于吗？请说明理由．

（3）点E在什么位置时，CF的长为？

Answer 1

【答案】（1）y＝﹣x2+x（0≤x≤1）；（2）CF的长不可能等于，理由详见解析；（3）AE＝或时，CF的长为．

【解析】

（1）根据正方形的内角为90°，以及同角的余角相等得出三角形的两个角相等，从而推知相似三角形：△ABE∽△ECF，得出比例关系，代入数值计算即可；

（2）把y＝代入（1）中的函数解析式，列出方程并解答；

（3）把y＝代入（1）中的函数解析式，列出方程并解答．

解：（1）∵正方形ABCD，

∴∠B＝∠C，∠BAE+∠BEA＝90°，

∵EF⊥AE，

∴∠BEA+∠CEF＝90°，

∴∠BAE＝∠CEF，

∴△ABE∽△ECF，

∴．

∵BE＝x，CF＝y，正方形ABCD的边长为1，

则CE＝1﹣x，

∴，

∴y＝﹣x2+x（0≤x≤1）．

（2）当CF的长等于时，＝﹣x2+x，

整理得：x2﹣x+＝0，

∵△＝（﹣1）2﹣4×1×＜0，

∴CF的长不可能等于；

（3）当CF的长为时，＝﹣x2+x，

解得：x＝或x＝，

故AE＝或时，CF的长为．