题目内容
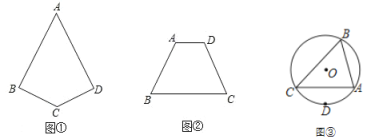
【题目】如图，四边形
是
的内接四边形．
，点
是
的中点，连接相交于点
，过点作
交
延长线于点
．
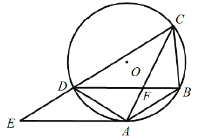
（1）求证：
为的切线；
（2）若
，
，求
的长．
【答案】（1）详见解析；（2）6
【解析】
（1）连接OA，由垂径定理易得OA⊥BD，再由AE∥BD，可得OA⊥AE，即可得证；
（2）由平行弦所夹的弧相等可推出BC=AD=AB=4，所以四边形ABCD为等腰梯形，过A作AP⊥CD于点P，过B作BQ⊥CD于点Q，易得PQ=AB=4，PD=CQ=0.5，然后利用勾股定理可求出BD，再证明四边形ABDE为平行四边形，可得AE=BD．
（1）如图，连接OA，
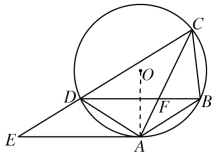
∵点A是
的中点，
∴OA⊥BD
又∵AE∥BD
∴OA⊥AE
∴AE为
的切线．
（2）∵AB∥CD
∴
∴BC=AD=AB=4
∴四边形ABCD为等腰梯形
如图所示，过A作AP⊥CD于点P，过B作BQ⊥CD于点Q，
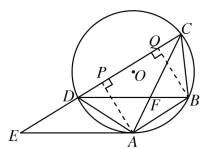
则四边形ABQP为矩形
∴PQ=AB=4
∵四边形ABCD为等腰梯形
∴AD=BQ，AP=BQ
∴Rt△ADP≌Rt△BCQ（HL）
∴PD=BQ=
在Rt△BCQ中，CQ2+BQ2=BC2
在Rt△BDQ中，
BD2=DQ2+BQ2=
∴BD=6
∵AE∥BD，AB∥DE
∴四边形ABDE为平行四边形
∴AE=BD=6
练习册系列答案
相关题目
【题目】某水果批发市场规定，批发苹果不少于
时，批发价为5元/
．小王携带现金4000元到这市场采购苹果，并以批发价买进．
（Ⅰ）根据题意，填表：
购买数量 |
|
|
|
|
花费 |
|
| ||
剩余现金 |
|
|
（Ⅱ）设购买的苹果为
，小王付款后还剩余现金
元．求关于
的函数解析式，并指出自变量的取值范围；
（Ⅲ）根据题意填空：若小王剩余现金为700元，则他购买__________的苹果．
