题目内容
【题目】如图,已知![]() 和
和![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转一周,连接
顺时针旋转一周,连接![]() 并延长与直线
并延长与直线![]() 相较于点
相较于点![]() ,则
,则![]() 的最小值为__________.
的最小值为__________.

【答案】![]()
【解析】
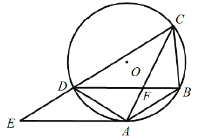
首先利用旋转模型易证△ABD≌△ACE,得到∠ABD=∠ACE,从而得出∠BPC=∠BAC=90°,即△BPC为直角三角形,BC为斜边,当∠BCP最小时,BP边长最小,以A为圆心,AD为半径画圆,可知当PC边与圆的下方相切时,∠BCP最小,此时四边形ADPE为矩形,利用勾股定理求出BD,减去PD即为BP的最小值.
∵∠BAC=∠DAE=90°,
∴∠CAE+∠BAE=∠BAD+∠BAE
∴∠CAE=∠BAD
在△ABD与△ACE中,
∵AD=AE,∠BAD=∠CAE,AB=AC
∴△ABD≌△ACE(SAS)
∴∠ABD=∠ACE
设AB,PC交于点F,
∵∠BFP=∠AFC
∴∠BPF=∠CAF=90°
∴∠DPE=90°
∴△BPC为直角三角形,BC为斜边,当∠BCP最小时,BP边长最小
如图所示,以A为圆心,AD为半径画圆,当PC边与圆的下方相切与点E时,∠BCP最小
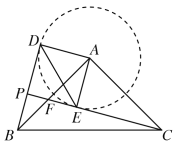
∵∠AEP=90°,∠DAE=90°,∠DPE=90°,
∴四边形ADPE为矩形
∴DP=AE=2,∠ADB=90°
∴在Rt△ABD中,BD=![]()
此时BP的最小值=BD-DP=![]()
故答案为:![]() .
.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目