题目内容
【题目】如图，在四边形ABCD中，已知AB∥CD，AD⊥AB，AD=2，AB+CD=4，点E为BC的中点．
（1）求四边形ABCD的面积；
（2）若AE⊥BC，求CD的长．
【答案】（1）S=4；（2）
.
【解析】
（1）作辅助线，构建三角形全等，将四边形ABCD的面积转化为三角形DAF的面积来解答；（2）连接AC，设CD=x，根据勾股定理列方程可解答．
解：（1）如图1，连接DE并延长，交AB的延长线于F，
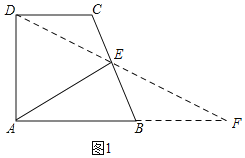
∵DC∥AB，
∴∠C=∠EBF，
∵CE=BE，∠DEC=∠FEB，
∴△DCE≌△FBE（ASA），
∴BF=DC，
∵AB+CD=4，
∴AB+BF=4=BF，
∴S四边形ABCD=S四边形ABED+S△DCE=S四边形ABED+S△EBF=S△DAF=
ADAF=×2×4=4；
（2）如图2，连接AC，
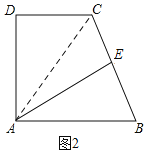
∵CE=BE，AE⊥BC，
∴AC=AB，
设CD=x，则AB=AC=4-x，
Rt△ACD中，由勾股定理得：CD2+AD2=AC2，
x2+22=（4-x）2，
解得：
，
∴
．
练习册系列答案
阅读快车系列答案
相关题目
